
【题目】如图,四边形![]() 是边长为2的正方形.
是边长为2的正方形.![]() 平面
平面![]() ,且
,且![]() .
.
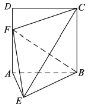
(1)求证:平面![]() 平面
平面![]() .
.
(2)线段![]() 上是否存在一点
上是否存在一点![]() ,使三棱锥
,使三棱锥![]() 的高
的高![]() 若存在,请求出
若存在,请求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
 高中必刷题系列答案
高中必刷题系列答案科目:高中数学 来源: 题型:
【题目】如图所示,某游乐园的一个摩天轮半径为10米,轮子的底部在地面上2米处,如果此摩天轮每20分钟转一圈,当摩天轮上某人经过![]() 处时开始计时(按逆时针方向转),
处时开始计时(按逆时针方向转),![]() (其中
(其中![]() 平行于地面).
平行于地面).
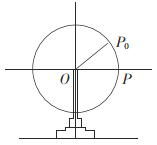
(1)求开始转动5分钟时此人相对于地面的高度.
(2)开始转动![]() 分钟时,摩天轮上此人经过点
分钟时,摩天轮上此人经过点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在以![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的五面体中,平面
为顶点的五面体中,平面![]() 平面
平面![]() ,
,![]() ,四边形
,四边形![]() 为平行四边形,且
为平行四边形,且![]() .
.
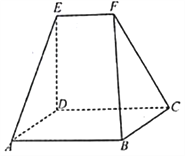
(1)求证:![]() ;
;
(2)若![]() ,
,![]() ,直线
,直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,求平面
,求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某机构为了了解不同年龄的人对一款智能家电的评价,随机选取了50名购买该家电的消费者,让他们根据实际使用体验进行评分.
(Ⅰ)设消费者的年龄为![]() ,对该款智能家电的评分为
,对该款智能家电的评分为![]() .若根据统计数据,用最小二乘法得到
.若根据统计数据,用最小二乘法得到![]() 关于
关于![]() 的线性回归方程为
的线性回归方程为![]() ,且年龄
,且年龄![]() 的方差为
的方差为![]() ,评分
,评分![]() 的方差为
的方差为![]() .求
.求![]() 与
与![]() 的相关系数
的相关系数![]() ,并据此判断对该款智能家电的评分与年龄的相关性强弱.
,并据此判断对该款智能家电的评分与年龄的相关性强弱.
(Ⅱ)按照一定的标准,将50名消费者的年龄划分为“青年”和“中老年”,评分划分为“好评”和“差评”,整理得到如下数据,请判断是否有![]() 的把握认为对该智能家电的评价与年龄有关.
的把握认为对该智能家电的评价与年龄有关.
好评 | 差评 | |
青年 | 8 | 16 |
中老年 | 20 | 6 |
附:线性回归直线![]() 的斜率
的斜率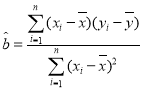 ;相关系数
;相关系数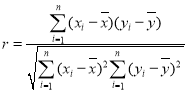 ,独立性检验中的
,独立性检验中的![]() ,其中
,其中![]() .
.
临界值表:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,设
,设![]() .
.
(1)若![]() ,记数列
,记数列![]() 的前
的前![]() 项和为
项和为![]() .①求证:数列
.①求证:数列![]() 为等差数列;②若不等式
为等差数列;②若不等式![]() 对任意的
对任意的![]() 都成立,求实数
都成立,求实数![]() 的最小值;
的最小值;
(2)若![]() ,且
,且![]() ,是否存在正整数
,是否存在正整数![]() ,使得无穷数列
,使得无穷数列![]() ,
,![]() ,
,![]() ,…成公差不为0的等差数列?若存在,给出数列
,…成公差不为0的等差数列?若存在,给出数列![]() 的一个通项公式;若不存在,请说明理由.
的一个通项公式;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】劳动教育是中国特色社会主义教育制度的重要内容,某高中计划组织学生参与各项职业体验,让学生在劳动课程中掌握一定劳动技能,理解劳动创造价值,培养劳动自立意识和主动服务他人、服务社会的情怀.学校计划下周在高一年级开设“缝纫体验课”,聘请“织补匠人”李阿姨给同学们传授织补技艺。高一年级有6个班,李阿姨每周一到周五只有下午第2节课的时间可以给同学们上课,所以必须安排有两个班合班上课,高一年级6个班“缝纫体验课”的不同上课顺序有( )
A.600种B.3600种C.1200种D.1800种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为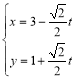 (
(![]() 为参数),在以坐标原点为极点,
为参数),在以坐标原点为极点,![]() 轴正半轴为极轴的极坐标系中,曲线
轴正半轴为极轴的极坐标系中,曲线![]() 的方程为
的方程为![]() .
.
(1)求曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设曲线![]() 与直线
与直线![]() 交于点
交于点![]() ,点
,点![]() 的坐标为(3,1),求
的坐标为(3,1),求![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com