
已知函数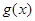 是
是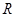 上的奇函数,且当
上的奇函数,且当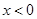 时
时 ,函数
,函数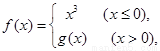 若
若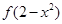 >
> ,则实数
,则实数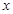 的取值范围是
的取值范围是
A.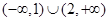 B.
B.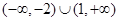
C.(1,2) D.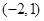
D
【解析】
试题分析:∵奇函数g(x)满足当x<0时,g(x)=-ln(1-x),
∴当x>0时,g(-x)=-ln(1+x)=-g(x),
得当x>0时,g(x)=-g(-x)=ln(1+x)
∴f(x)的表达式为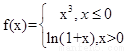 ,
,
∵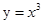 在(-∞,0)上是增函数,y=ln(1+x)在(0,+∞)上是增函数,
在(-∞,0)上是增函数,y=ln(1+x)在(0,+∞)上是增函数,
∴f(x)在其定义域上是增函数,
由此可得: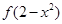 >
>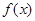 等价于
等价于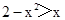 ,解之得-2<x<1,
,解之得-2<x<1,
故选D。
考点:本题主要考查分段函数的概念,函数的奇偶性、单调性,简单不等式的解法。
点评:中档题,涉及抽象函数不等式问题,一般的要通过研究函数的单调性,转化成具体不等式求解。本题定义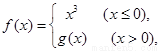 人为地增大了难度,易于出错。
人为地增大了难度,易于出错。


科目:高中数学 来源:2010-2011学年福建省高三上学期期中考试数学理卷 题型:选择题
已知函数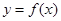 是
是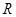 上的奇函数,函数
上的奇函数,函数 是
是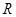 上的偶函数,且
上的偶函数,且 ,当
,当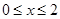 时,
时, ,则
,则 的值为( )
的值为( )
A. B.
B. C.
C.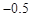 D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com