
(理科做)
甲、乙两队进行一场排球比赛.根据以往经验,单局比赛甲队胜乙队的概率为0.6,本场比赛采用五局三胜制,即先胜三局的队获胜,比赛结束.设各局比赛相互间没有影响.令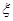 为本场比赛的局数.求
为本场比赛的局数.求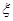 的概率分布和数学期望.(精确到0.0001)
的概率分布和数学期望.(精确到0.0001)
科目:高中数学 来源:河北省保定市2009届高三上学期调研考试数学试题(Word版) 题型:044
美国次贷危机引发2008年全球金融动荡,波及中国两大股市.甲、乙、丙三人打算趁目前股市低迷之际“抄底”.若三人商定在圈定的10支股票中各自随机购买一支(假定购买时每支股票的基本情况完全相同).
(1)求甲、乙、丙三人恰好买到一支相同股票的概率;
(2)求甲、乙、丙三人中至少有两人买到一支相同股票的概率;
(3)(只理科做)由于国家采取了积极的救市措施,股市渐趋回暖.若某人今天按上一交易日的收盘价20元/股买人1000股,且预计今天收盘时,该股涨停(比上一交易日的收盘价上涨10%)的概率为0.5,持平的概率为0.2,否则将下跌5%,求该人今天获利的数学期望(不考虑交易税).
查看答案和解析>>
科目:高中数学 来源:2010年新疆乌鲁木齐高二上学期期中考试数学试卷 题型:解答题
现有7名同学去参加一个活动,分别求出以下不同要求的方法数(以下各小题写出必要的计算公式,最终结果用数字作答)
(1)排队时7名同学中的丙不站在中间的排法
(2) 排队时7名同学中的甲、乙、丙三名同学各不相邻的排法
(3)排队时7名同学中的甲不能站在最前并且已不能站在最后的排法(理科学生做)
(4)7名学生选出3名代表发言,甲,乙,丙三名同学至多两人个入选的选法(理科学生做)
7名学生中选出3名代表发言,甲、乙只有一人入选的选法有多少?(文科学生做)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com