Question

【题目】在如图所示的几何体中，AE⊥平面ABC，CD∥AE，F是BE的中点，AC=BC=1，∠ACB=90°，AE=2CD=2．
证明DF⊥平面ABE；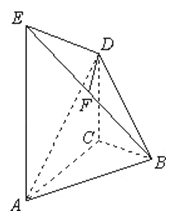

Answer 1

【答案】解：取AB的中点G，连接CG、FG．
因为CD∥AE，GF∥AE，所以CD∥GF．
又因为CD=1，，所以CD=GF．
所以四边形CDFG是平行四边形，DF∥CG．
在等腰Rt△ACB中，G是AB的中点，所以CG⊥AB．
因为EA⊥平面ABC，CG平面ABC，所以EA⊥CG．
而AB∩EA=A，所以CG⊥平面ABE．
又因为DF∥CG，所以DF⊥平面ABE．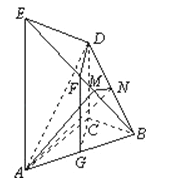

【解析】将DF平移到CG的位置，欲证DF⊥平面ABE，即证CG⊥平面ABE，根据线面垂直的判定定理可知，只需证CG与平面ABE内的两相交直线垂直即可；
【考点精析】解答此题的关键在于理解平面与平面之间的位置关系的相关知识，掌握两个平面平行没有交点；两个平面相交有一条公共直线．