
【题目】如图,四边形ABCD中,AB=AD=CD=1,BD= ![]() ,BD⊥CD.将四边形ABCD沿对角线BD折成四面体A′﹣BCD,使平面A′BD⊥平面BCD,则下列结论正确的是( )
,BD⊥CD.将四边形ABCD沿对角线BD折成四面体A′﹣BCD,使平面A′BD⊥平面BCD,则下列结论正确的是( ) 
A.A′C⊥BD
B.∠BA′C=90°
C.CA′与平面A′BD所成的角为30°
D.四面体A′﹣BCD的体积为 ![]()
科目:高中数学 来源: 题型:
【题目】《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑. 如图,在阳马P﹣ABCD中,侧棱PD⊥底面ABCD,且PD=CD,E为PC中点,点F在PB上,且PB⊥平面DEF,连接BD,BE.
(Ⅰ)证明:DE⊥平面PBC;
(Ⅱ)试判断四面体DBEF是否为鳖臑,若是,写出其每个面的直角(只需写出结论);若不是,说明理由;
(Ⅲ)已知AD=2, ![]() ,求二面角F﹣AD﹣B的余弦值.
,求二面角F﹣AD﹣B的余弦值.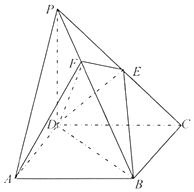
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某成衣批发店为了对一款成衣进行合理定价,将该款成衣按事先拟定的价格进行试销,得到了如下数据:
批发单价x(元) | 80 | 82 | 84 | 86 | 88 | 90 |
销售量y(件) | 90 | 84 | 83 | 80 | 75 | 68 |
(1)求回归直线方程 ![]() ,其中
,其中 ![]()
(2)预测批发单价定为85元时,销售量大概是多少件?
(3)假设在今后的销售中,销售量与批发单价仍然服从(1)中的关系,且该款成衣的成本价为40元/件,为使该成衣批发店在该款成衣上获得更大利润,该款成衣单价大约定为多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆 ![]() 的左右顶点分别为A,B,点P在椭圆上且异于A,B两点,O为坐标原点.
的左右顶点分别为A,B,点P在椭圆上且异于A,B两点,O为坐标原点.
(1)若直线AP与BP的斜率之积为 ![]() ,求椭圆的离心率;
,求椭圆的离心率;
(2)若|AP|=|OA|,证明直线OP的斜率k满足|k|> ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的几何体中,AE⊥平面ABC,CD∥AE,F是BE的中点,AC=BC=1,∠ACB=90°,AE=2CD=2.
证明DF⊥平面ABE;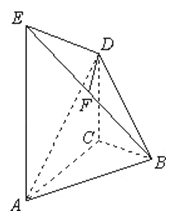
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD与ABEF均为矩形,BC=BE=2AB,二面角E﹣AB﹣C的大小为 ![]() .现将△ACD绕着AC旋转一周,则在旋转过程中,( )
.现将△ACD绕着AC旋转一周,则在旋转过程中,( ) 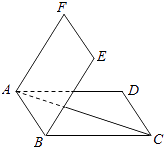
A.不存在某个位置,使得直线AD与BE所成的角为 ![]()
B.存在某个位置,使得直线AD与BE所成的角为 ![]()
C.不存在某个位置,使得直线AD与平面ABEF所成的角为 ![]()
D.存在某个位置,使得直线AD与平面ABEF所成的角为 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对应的边分别为a,b,c,且(2a﹣c)cosB=bcosC. (Ⅰ)求角B的大小;
(Ⅱ)若a=2,c=3,求sinC的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com