现有6名奥运会志愿者,其中志愿者A1,A2通晓日语,B1,B2通晓俄语,C1,C2通晓韩语.从中选出通晓日语、俄语和韩语的志愿者各1名,组成一个小组.
(Ⅰ)求A1被选中的概率;
(Ⅱ)求B1和C1不全被选中的概率.
(Ⅲ)若6名奥运会志愿者每小时派俩人值班,现有俩名只会日语的运动员到来,求恰好遇到A1,A2的概率.
【答案】
分析:(Ⅰ)先用列举法,求出从8人中选出日语、俄语和韩语志愿者各1名,所有一切可能的结果对应的基本事件总个数,再列出A
1恰被选中这一事件对应的基本事件个数,然后代入古典概型公式,即可求解.
(Ⅱ)我们可利用对立事件的减法公式进行求解,即求出“B
1,C
1不全被选中”的对立事件“B
1,C
1全被选中”的概率,然后代入对立事件概率减法公式,即可得到结果.
(III)根据6名奥运会志愿者每小时派俩人值班,我们可以判断A
1,A
2值班的概率.
解答:解:(Ⅰ)从6人中选出日语、俄语和韩语志愿者各1名,其一切可能的结果组成的基本事件空间Ω={(A
1,B
1,C
1),(A
1,B
1,C
2),(A
1,B
2,C
1),(A
1,B
2,C
2),(A
2,B
1,C
1),(A
2,B
1,C
2),(A
2,B
2,C
1),(A
2,B
2,C
2),
由8个基本事件组成.由于每一个基本事件被抽取的机会均等,
因此这些基本事件的发生是等可能的.
用M表示“A
1恰被选中”这一事件,则M={(A
1,B
1,C
1),(A
1,B
1,C
2),(A
1,B
2,C
1),(A
1,B
2,C
2)}
事件M由4个基本事件组成,因而

.
(Ⅱ)用N表示“B
1,C
1不全被选中”这一事件,则其对立事件
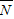
表示“B
1,C
1全被选中”这一事件,由于
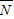
={(A
1,B
1,C
1),(A
2,B
1,C
1)},事件
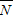
有2个基本事件组成,
所以

,由对立事件的概率公式得
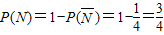
.
(Ⅲ)∵6名奥运会志愿者每小时派俩人值班,共有C
62=15种情况
而恰好遇到A
1,A
2的情况只有1种
故恰好遇到A
1,A
2的概率p=
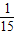 点评:
点评:本题考查的知识点是古典概型,古典概型要求所有结果出现的可能性都相等,强调所有结果中每一结果出现的概率都相同.弄清一次试验的意义以及每个基本事件的含义是解决问题的前提,正确把握各个事件的相互关系是解决问题的关键.解决问题的步骤是:计算满足条件的基本事件个数,及基本事件的总个数,然后代入古典概型计算公式进行求解

 .
.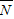 表示“B1,C1全被选中”这一事件,由于
表示“B1,C1全被选中”这一事件,由于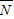 ={(A1,B1,C1),(A2,B1,C1)},事件
={(A1,B1,C1),(A2,B1,C1)},事件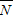 有2个基本事件组成,
有2个基本事件组成, ,由对立事件的概率公式得
,由对立事件的概率公式得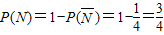 .
.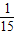


 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案