
【题目】如图,设椭圆![]() :
: ![]() 的离心率为
的离心率为![]() ,
, ![]() 分别为椭圆
分别为椭圆![]() 的左、右顶点,
的左、右顶点, ![]() 为右焦点,直线
为右焦点,直线![]() 与
与![]() 的交点到
的交点到![]() 轴的距离为
轴的距离为![]() ,过点
,过点![]() 作
作![]() 轴的垂线
轴的垂线![]() ,
, ![]() 为
为![]() 上异于点
上异于点![]() 的一点,以
的一点,以![]() 为直径作圆
为直径作圆![]() .
.
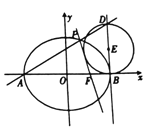
(1)求![]() 的方程;
的方程;
(2)若直线![]() 与
与![]() 的另一个交点为
的另一个交点为![]() ,证明:直线
,证明:直线![]() 与圆
与圆![]() 相切.
相切.
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:高中数学 来源: 题型:
【题目】20名学生某次数学考试成绩(单位:分)的频率分布直方图如图: 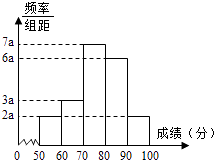
(1)求频率分布直方图中a的值;
(2)分别求出成绩落在[50,60)与[60,70)中的学生人数;
(3)从成绩在[50,70)的学生任选2人,求此2人的成绩都在[60,70)中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数f(x)为定义在R上的奇函数,且在(0,+∞)内是增函数,又f(2)=0,则不等式x5f(x)>0的解集为( )
A.(﹣2,0)∪(2,+∞)
B.(﹣∞,﹣2)∪(0,2)
C.(﹣2,0)∪(0,2)
D.(﹣∞,﹣2)∪(2,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司的两个部门招聘工作人员,应聘者从 T1、T2两组试题中选择一组参加测试,成绩合格者可签约.甲、乙、丙、丁四人参加应聘考试,其中甲、乙两人选择使用试题 T1 , 且表示只要成绩合格就签约;丙、丁两人选择使用试题 T2 , 并约定:两人成绩都合格就一同签约,否则两人都不签约.已知甲、乙考试合格的概率都是 ![]() ,丙、丁考试合格的概率都是
,丙、丁考试合格的概率都是 ![]() ,且考试是否合格互不影响.
,且考试是否合格互不影响.
(1)求丙、丁未签约的概率;
(2)记签约人数为 X,求 X的分布列和数学期望EX.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com