
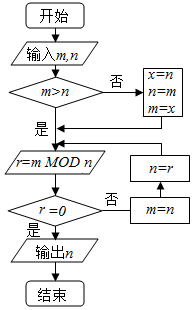
分析 根据已知中的程序框图,可得该程序的功能是利用辗转相除法,求m,n的最大公约数,模拟程序的运算过程,可得答案.
解答 解:根据已知中的程序框图,可得该程序的功能是利用辗转相除法,求m,n的最大公约数,
当输入n=251,m=15时,先交换m,n的值,故m=251,n=15,
第一次执行循环体后,r=11,不满足退出循环的条件,故m=15,n=11;
再次执行循环体后,r=4,不满足退出循环的条件,故m=11,n=4;
再次执行循环体后,r=3,不满足退出循环的条件,故m=4,n=3;
再次执行循环体后,r=1,不满足退出循环的条件,故m=3,n=1;
再次执行循环体后,r=0,满足退出循环的条件,
故输出的n值为1,
故答案为:1.
点评 本题考查了程序框图的应用问题,解题时应模拟程序框图的运行过程,以便得出正确的结论,是中档题.


 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:高中数学 来源:2016-2017学年湖南益阳市高二9月月考数学(理)试卷(解析版) 题型:解答题
为了响应国家号召,某地决定分批建设保障性住房供给社会.首批计划用100万元购得一块土地,该土地可以建造每层1 000平方米的楼房,楼房的每平方米建筑费用与建筑高度有关,楼房每升高一层,整层楼每平方米建筑费用提高20元.已知建筑第5层楼房时,每平方米建筑费用为800元.
(1)若建筑第x层楼时,该楼房综合费用为y万元(综合费用是建筑费用与购地费用之和),写出y=f(x)的表达式;
(2)为了使该楼房每平方米的平均综合费用最低,应把楼层建成几层?此时平均综合费用为每平方米多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,A,B,C,D为平面四边形ABCD的四个内角.
如图,A,B,C,D为平面四边形ABCD的四个内角.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
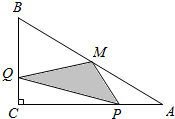 如图,△ABC中,∠C=90°,M是AB的中点,动点P从点A出发,沿AC方向匀速运动到终点C,动点Q从点C出发,沿CB方向匀速运动到终点B.已知P,Q两点同时出发,并同时到达终点,连接MP,MQ,PQ.在整个运动过程中,△MPQ的面积大小变化情况是( )
如图,△ABC中,∠C=90°,M是AB的中点,动点P从点A出发,沿AC方向匀速运动到终点C,动点Q从点C出发,沿CB方向匀速运动到终点B.已知P,Q两点同时出发,并同时到达终点,连接MP,MQ,PQ.在整个运动过程中,△MPQ的面积大小变化情况是( )| A. | 一直增大 | B. | 一直减小 | C. | 先减小后增大 | D. | 先增大后减小 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com