解:(1)g(1)+g(3)+g(5)+g(7)=1+3+5+7+16;g(1)+g(2)+g(3)+g(4)=1+1+3+1=6;g(2)+g(4)+g(6)+g(8)=1+1+3+1=6
(2)g(1)+g(3)+g(5)+…+g(2k-1)=
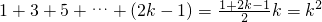
证明:∵2k=2•k∴2k中的最大奇因数即k为中的最大奇因数
∴g(2)+g(4)+g(6)+…+g(2
n)=g(2•1)+g(2•2)+g(2•3)+…+g(2•2
n-1)=g(1)+g(2)+g(3)+…+g(2
n-1)
(3)当n≥2时,f(n)=g(1)+g(2)+g(3)+…+g(2
n)=g(1)+g(3)+g(5)+…+g(2
n-1)+g(2)+g(4)+…+g(2
n)=1+3+5+…+(2
n-1)+g(1)+g(2)+g(3)+…+g(2
n-1)=
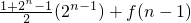
=4
n-1+f(n-1)
即f(n)-f(n-1)=4
n-1∴f(3)-f(2)=4
2,f(4)-f(3)=4
3,
…f(n)-f(n-1)=4
n-1可得f(n)=4
2+4
3+…+4
n-1+f(2)=
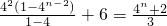
当n=1时,f(1)=g(1)+g(2)=1+1=2也成立,
∴
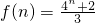
n∈N
*分析:(1)g(1)+g(3)+g(5)+g(7)=1+3+5+7+16;g(1)+g(2)+g(3)+g(4)=1+1+3+1=6,g(2)+g(4)+g(6)+g(8)=1+1+3+1=6
(2)g(1)+g(3)+g(5)+…+g(2k-1)=1+3+5+…(2k-1),利用等差数列的求和公式可求
由2k=2•k可得2k中的最大奇因数即k为中的最大奇因数,从而可得g(2)+g(4)+g(6)+…+g(2
n)=g(2•1)+g(2•2)+g(2•3)+…+g(2•2
n-1)=g(1)+g(2)+g(3)+…+g(2
n-1)
(3)由于f(n)=g(1)+g(2)+g(3)+…+g(2
n)=[g(1)+g(3)+g(5)+…+g(2
n-1)]+[g(2)+g(4)+…+g(2
n)]=1+3+5+…+(2
n-1)+g(1)+g(2)+g(3)+…+g(2
n-1),由(2)及等差数列的 求和公式可得f(n)=f(n-1)+4
n-1,利用叠加可求
点评:本题考查数列的性质和应用,叠加求解数列的通项公式,等差数列的求和公式,解题时要注意公式的灵活运用,合理地进行等价转化.

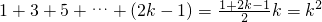
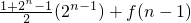 =4n-1+f(n-1)
=4n-1+f(n-1)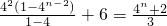
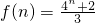 n∈N*
n∈N*
