已知数列{an}是等差数列,a1=2,且a2,a4,a8成等比数列.
( I)求等差数列{an}的通项公式;
(II)如果数列{bn}是等比数列,且b1=a2,b2=a4,求{bn}的前n项和Sn.
解:(I)因为数列{a
n}是等差数列,设其公差为d,a
1=2,
则a
2=2+d,a
4=2+3d,a
8=2+7d.
由a
2,a
4,a
8成等比数列,得a
42=a
2a
8,
即(2+3d)
2=(2+d)(2+7d)
解得d=0或d=2,
所以a
n=2或a
n=2n.
(II)①当a
n=2时,b
1=a
2=2,b
2=a
4=2,公比q=1,
{b
n}的前n项和S
n=nb
1=2n;
②当a
n=2n时,b
1=a
2=4,b
2=a
4=8,公比q=2,
{b
n}的前n项和
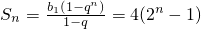
.
分析:(I)已知数列{a
n}是等差数列,设出公差d,又a
1=2,由a
2,a
4,a
8成等比数列得到关于d的一元二次方程,求出d有两解,分别就两个d求出两个通项公式;
(II)由(I)可得a
2,a
4,有两组解,又b
1=a
2,b
2=a
4,可得两组b
1,b
2,又知数列{b
n}是等比数列,可求出两个公比q,选择含有首项和公比的等比数列的前n项和公式,就两种情况分别求出即可.
点评:本题主要考查等差数列的通项公式和等比数列的前n项和公式,已知数列为等差数列,求通项公式,求首项和公差即可,本题公差有两个,所以有两个通项公式;求等比数列的前n项和时,由已知准确选择公式.

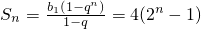 .
.

 百年学典课时学练测系列答案
百年学典课时学练测系列答案