
已知平行四边形ABCD中,点E为CD的中点, =m
=m ,
, =n
=n (m•n≠0),若
(m•n≠0),若 ∥
∥ ,则
,则 =___________________.
=___________________.
 巧学巧练系列答案
巧学巧练系列答案 课课练江苏系列答案
课课练江苏系列答案科目:高中数学 来源: 题型:
等腰Rt△ACB,AB=2, .以直线AC为轴旋转一周得到一个圆锥,D为圆锥底面一点,BD⊥CD,CH⊥AD于点H,M为AB中点,则当三棱锥C﹣HAM的体积最大时,CD的长为( )
.以直线AC为轴旋转一周得到一个圆锥,D为圆锥底面一点,BD⊥CD,CH⊥AD于点H,M为AB中点,则当三棱锥C﹣HAM的体积最大时,CD的长为( )
|
| A. |
| B. |
| C. |
| D. |
|
查看答案和解析>>
科目:高中数学 来源: 题型:
在平面直角坐标系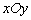 中,从曲线
中,从曲线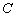 上一点
上一点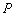 做
做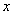 轴和
轴和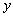 轴的垂线,垂足分别为
轴的垂线,垂足分别为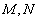 ,点
,点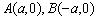 (
( 为常数),且
为常数),且 (
(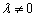 )
)
(1)求曲线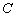 的轨迹方程,并说明曲线
的轨迹方程,并说明曲线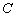 是什么图形;
是什么图形;
(2)当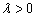 且
且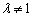 时,将曲线
时,将曲线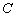 绕原点逆时针旋转
绕原点逆时针旋转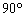 得到曲线
得到曲线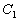 ,曲线
,曲线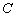 与曲线
与曲线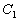 四个交点按逆时针依次为
四个交点按逆时针依次为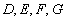 ,且点
,且点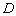 在一象限
在一象限
①证明:四边形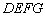 为正方形; ②若
为正方形; ②若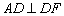 ,求
,求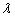 值.
值.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知抛物线 :
: 和
和 :
:
 的焦点分别为
的焦点分别为 ,
, 交于
交于 两点(
两点( 为坐标原点),且
为坐标原点),且
 .
.
(1)求抛物线 的方程;
的方程;
(2)过点 的直线交
的直线交 的下半部分于点
的下半部分于点 ,交
,交 的左半部分于点
的左半部分于点 ,点
,点 坐标为
坐标为 ,求△
,求△ 面积的最小值.
面积的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com