
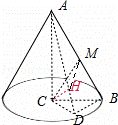
等腰Rt△ACB,AB=2, .以直线AC为轴旋转一周得到一个圆锥,D为圆锥底面一点,BD⊥CD,CH⊥AD于点H,M为AB中点,则当三棱锥C﹣HAM的体积最大时,CD的长为( )
.以直线AC为轴旋转一周得到一个圆锥,D为圆锥底面一点,BD⊥CD,CH⊥AD于点H,M为AB中点,则当三棱锥C﹣HAM的体积最大时,CD的长为( )
|
| A. |
| B. |
| C. |
| D. |
|
C.
【解析】根据题意,得
∵AC⊥平面BCD,BD⊂平面BCD,∴AC⊥BD,
∵CD⊥BD,AC∩CD=C,∴BD⊥平面ACD,可得BD⊥CH,
∵CH⊥AD,AD∩BD=D,∴CH⊥平面ABD,可得CH⊥AB,
∵CM⊥AB,CH∩CM=C,∴AB⊥平面CMH,
因此,三棱锥C﹣HAM的体积V=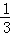 S△CMH×AM=
S△CMH×AM=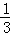 S△CMH由此可得,当S△CMH达到最大值时,三棱锥C﹣HAM的体积最大
S△CMH由此可得,当S△CMH达到最大值时,三棱锥C﹣HAM的体积最大
设∠BCD=θ,则Rt△BCD中,BC=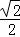 AB=
AB=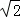
可得CD=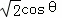 ,BD=
,BD=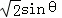
Rt△ACD中,根据等积转换得CH=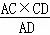 =
=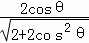
Rt△ABD∽Rt△AHM,得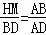 ,所以HM=
,所以HM=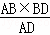 =
=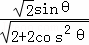
因此,S△CMH=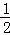 CH•HM=
CH•HM=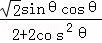 =
=
∵4+2tan2θ≥4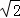 tanθ,
tanθ,
∴S△CMH= ≤
≤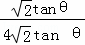 =
=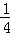 ,
,
当且仅当tanθ=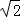 时,S△CMH达到最大值,三棱锥C﹣HAM的体积同时达到最大值.
时,S△CMH达到最大值,三棱锥C﹣HAM的体积同时达到最大值.
∵tanθ=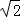 >0,可得sinθ=
>0,可得sinθ=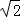 cosθ>0
cosθ>0
∴结合sin2θ+cos2θ=1,解出cos2θ=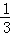 ,可得cosθ=
,可得cosθ=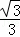 (舍负)
(舍负)
由此可得CD=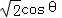 =
=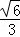 ,
,
即当三棱锥C﹣HAM的体积最大时,CD的长为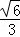
故选:C


科目:高中数学 来源: 题型:
如图,AB是⊙O的直径,AC是弦,直线CE和⊙O切于点C,AD丄CE,垂足为D.
(I) 求证:AC平分∠BAD;
(II) 若AB=4AD,求∠BAD的大小.

查看答案和解析>>
科目:高中数学 来源: 题型:
已知AB是圆O的直径,C为圆O上一点,CD⊥AB于点D,
弦BE与CD、AC 分别交于点M、N,且MN = MC

(1)求证:MN = MB;
(2)求证:OC⊥MN。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com