
分析 (1)通过φ=$\frac{π}{2}$时,化简函数的解析式,利用函数的奇偶性的定义,判断f(x)是偶函数;
(2)利用偶函数的定义,化简方程,通过求解三角方程求解即可.
解答 (1)证明:当φ=$\frac{π}{2}$时,f(x)=12sin(2x+$\frac{π}{2}$)=12cos2x,f(-x)=f(x),f(x)是偶函数;
(2)解:由题意:f(-x)=f(x),
可得12sin(-2x+φ)=12sin(2x+φ)对一切实数x成立,
-2x+φ=2x+φ+2kπ,或-2x+φ=π-(2x+φ)+2kπ( k∈Z)对一切实数x成立,
所以φ=kπ+$\frac{π}{2}$,k∈Z,
f(x)为偶函数的φ值的集合是{φ|φ=kπ+$\frac{π}{2}$,k∈Z}.
点评 本题考查三角函数的简单性质的应用,三角方程的解法,考查计算能力.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
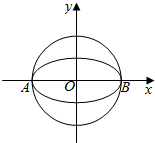 已知椭圆$W:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率为$\frac{{\sqrt{3}}}{2}$,其左顶点A在圆O:x2+y2=16上.
已知椭圆$W:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率为$\frac{{\sqrt{3}}}{2}$,其左顶点A在圆O:x2+y2=16上.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 喜爱古典音乐 青年 | 喜爱 | 不喜爱 |
| 男青年 | 46 | 30 |
| 女青年 | 20 | 50 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com