已知数列{an}中,a1=2,点(an,an+1)在直线y=2x上.数列{bn}满足bn+2-2bn+1+bn=0(n∈N+),且b3=11,S9=153.
bn+2-2bn+1+bn=0
(Ⅰ)求数列{an},{bn}的通项;
(Ⅱ)设cn=an•bn,{cn}的前n项和为Tn,求Tn.
【答案】
分析:(I)由题意可得a
n+1=2a
n,即数列a
n为等比数列,代入等比数列的通项可求a
n;由b
n+2-2b
n+1+b
n=0⇒b
n+2-b
n+1=b
n+1-b
n,从而可得数列b
n为等差数列,结合题中所给条件可求公差d,首项b
1,进一步可求数列的通项.
(II)由(I)可知数列a
nb
n分别为等差、等比数列,对数列c
n求和用错位相减.
解答:解:(Ⅰ)点(a
n,a
n+1)在直线y=2x上,
∴
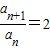
,数列{a
n}为等比数列,
又a
1=2,∴a
n=2
n.
∵b
n+2-2b
n+1+b
n=0,∴b
n+2-b
n+1=b
n+1-b
n═b
2-b
1即数列{b
n}为等差数列,∵b
1=11,S
9=153,设首项为b
1,公差为d.
b
1+2d=1
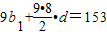
,解得b
1=5,d=3,∴b
n=3n+2
(Ⅱ)c
n=b
n•a
n=(3n+2)•2
n∴T
n=5•2+8•2
2++(3n+2)•2
n①
2T
n=5•2
2+8•2
3++(3n+2)•2
n+1②
①-②得:-T
n=5•2+3•2
2++3•2
n-(3n+2)•2
n+1∴T
n=(3n-1)•2
n+1+2
点评:本题主要考查了等差数列及等比数列的通项公式、定义,属于对基本概念、基本公式的考查,还考查了求和方法的乘公比错位相减求和,属于基础题中档题.

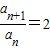 ,数列{an}为等比数列,
,数列{an}为等比数列,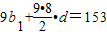 ,解得b1=5,d=3,∴bn=3n+2
,解得b1=5,d=3,∴bn=3n+2
