
甲乙丙丁4人玩传球游戏,持球者将球等可能的传给其他3人,若球首先从甲传出,经过3次传球.
(1)求球恰好回到甲手中的概率;
(2)设乙获球(获得其他游戏者传的球)的次数为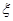 ,求
,求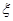 的分布列及数学期望.
的分布列及数学期望.
(1)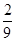 ;(2)分布列详见解析,
;(2)分布列详见解析,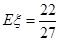 .
.
解析试题分析:本题主要考查古典概型和离散型随机变量的分布列和数学期望等数学知识,考查学生的分析问题解决问题的能力和计算能力.第一问,利用古典概型先求出经过3次传球的传球方法共27种,再求3次传球后,求恰好回到甲手中的种数,相除得到概率值;第二问,先分别求出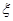 的3种情况的概率,概率的分子可以用树状图数出来,列出分布列,利用
的3种情况的概率,概率的分子可以用树状图数出来,列出分布列,利用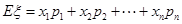 求出数学期望.
求出数学期望.
试题解析:⑴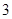 次传球,传球的方法共有
次传球,传球的方法共有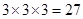 种,
种,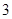 次传球结束时,球恰好回到甲手中的传球方法为
次传球结束时,球恰好回到甲手中的传球方法为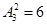 种,故所求概率为
种,故所求概率为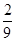 5分
5分
⑵易知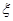 的所有可能取值为
的所有可能取值为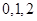 6分
6分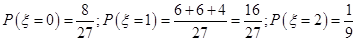 , 9分
, 9分
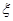 的分布列为
的分布列为
10分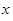
0 1 2 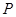
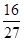
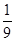
因此, . 12分
. 12分
考点:1.古典概型;2.离散型随机变量的分布列和数学期望.


科目:高中数学 来源: 题型:解答题
已知一个矩形由三个相同的小矩形拼凑而成(如图所示),用三种不同颜色给3个小矩形涂色,每个小矩形只涂一种颜色,求:
(1)3个矩形都涂同一颜色的概率;
(2)3个小矩形颜色都不同的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知直线l1:x-2y-1=0,直线l2:ax-by+1=0,其中a,b∈{1,2,3,4,5,6}.
(1) 求直线l1与l2相交的概率;
(2) 求直线l1与l2的交点位于第一象限的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
判断下列命题正确与否.
(1)先后掷两枚质地均匀的硬币,等可能出现“两个正面”“两个反面”“一正一反”三种结果;
(2)某袋中装有大小均匀的三个红球、两个黑球、一个白球,任取一球,那么每种颜色的球被摸到的可能性相同;
(3)从-4,-3,-2,-1,0,1,2中任取一数,取到的数小于0与不小于0的可能性相同;
(4)分别从3名男同学、4名女同学中各选一名代表,男、女同学当选的可能性相同.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
为迎接2013年“两会”(全国人大3月5日-3月18日、全国政协3月3日-3月14日)的胜利召开,某机构举办猜奖活动,参与者需先后回答两道选择题,问题A有四个选项,问题B有五个选项,但都只有一个选项是正确的,正确回答问题A可获奖金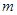 元,正确回答问题B可获奖金
元,正确回答问题B可获奖金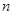 元.活动规定:参与者可任意选择回答问题的顺序,如果第一个问题回答错误,则该参与者猜奖活动中止.假设一个参与者在回答问题前,对这两个问题都很陌生,试确定哪种回答问题的顺序能使该参与者获奖金额的期望值较大.
元.活动规定:参与者可任意选择回答问题的顺序,如果第一个问题回答错误,则该参与者猜奖活动中止.假设一个参与者在回答问题前,对这两个问题都很陌生,试确定哪种回答问题的顺序能使该参与者获奖金额的期望值较大.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数y=x-1,令x=―4,―3,―2,-1,0,1,2,3,4,可得函数图象上的九个点,在这九个点中随机取出两个点P1(x1,y1),P2(x2,y2),
(1)求P1,P2两点在双曲线xy=6上的概率;
(2)求P1,P2两点不在同一双曲线xy=k(k≠0)上的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
中国共产党第十八次全国代表大会期间,某报刊媒体要选择两名记者去进行专题采访,现有记者编号分别为1,2,3,4,5的五名男记者和编号分别为6,7,8,9的四名女记者.要从这九名记者中一次随机选出两名,每名记者被选到的概率是相等的,用符号(x,y)表示事件“抽到的两名记者的编号分别为x、y,且x<y”.
(1)共有多少个基本事件?并列举出来;
(2)求所抽取的两名记者的编号之和小于17但不小于11或都是男记者的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某商店储存的50个灯泡中,甲厂生产的灯泡占60%,乙厂生产的灯泡占40%,甲厂生产的灯泡的一等品率是90%,乙厂生产的灯泡的一等品率是80%.
(1)若从这50个灯泡中随机抽取出1个灯泡(每个灯泡被取出的机会均等),则它是甲厂生产的一等品的概率是多少?
(2)若从这50个灯泡中随机抽取出2个灯泡(每个灯泡被取出的机会均等),这2个灯泡中是甲厂生产的一等品的个数记为ξ,求E(ξ)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在一次数学测验后,班级学委对选答题的选题情况进行了统计,如下表:
| | 几何证明选讲 | 坐标系与 参数方程 | 不等式选讲 | 合计 |
| 男同学(人数) | 12 | 4 | 6 | 22 |
| 女同学(人数) | 0 | 8 | 12 | 20 |
| 合计 | 12 | 12 | 18 | 42 |
| | 几何类 | 代数类 | 总计 |
| 男同学(人数) | 16 | 6 | 22 |
| 女同学(人数) | 8 | 12 | 20 |
| 总计 | 24 | 18 | 42 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com