
已知一个矩形由三个相同的小矩形拼凑而成(如图所示),用三种不同颜色给3个小矩形涂色,每个小矩形只涂一种颜色,求:
(1)3个矩形都涂同一颜色的概率;
(2)3个小矩形颜色都不同的概率.
(1)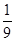 ;(2)
;(2)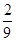 .
.
解析试题分析:(1)利用分步乘法原理即可得出涂完三个矩形共有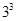 种方法,而3个矩形都涂同一颜色的方法只有三种,利用古典概型的概率计算公式即可得出;(2)“3个小矩形颜色都不同”相当于把三种颜色的全排列数,即
种方法,而3个矩形都涂同一颜色的方法只有三种,利用古典概型的概率计算公式即可得出;(2)“3个小矩形颜色都不同”相当于把三种颜色的全排列数,即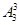 种涂法.利用古典概型的概率计算公式即可得出.
种涂法.利用古典概型的概率计算公式即可得出.
试题解析:(1)由题意可知:用三种不同颜色给3个小矩形涂色,每个小矩形只涂一种颜色,可以分三步去完成:
涂第一个矩形可有三种方法,涂第二个矩形可有三种方法,涂第三个矩形可有三种方法,
由分步乘法原理可得涂完三个矩形共有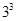 =27种方法,其中3个矩形都涂同一颜色的方法只有三种.
=27种方法,其中3个矩形都涂同一颜色的方法只有三种.
设“3个矩形都涂同一颜色”为事件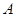 ,则
,则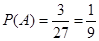 .
.
(2)由(1)可知:三种不同颜色给3个小矩形涂色,每个小矩形只涂一种颜色,方法共有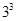 .
.
设“3个小矩形颜色都不同”为事件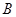 ,则事件
,则事件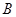 包括
包括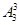 种涂法.
种涂法.
由古典概型的概率计算公式可得: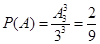 .
.
考点:1、古典概型的概率;2、排列的应用.


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:高中数学 来源: 题型:解答题
一批产品需要进行质量检验,检验方案是:先从这批产品中任取4件作检验,这4件产品中优质品的件数记为n.如果n=3,再从这批产品中任取4件作检验,若都为优质品,则这批产品通过检验;如果n=4,再从这批产品中任取1件作检验,若为优质品,则这批产品通过检验;其他情况下,这批产品都不能通过检验.
假设这批产品的优质品率为50%,即取出的产品是优质品的概率都为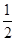 ,且各件产品是否为优质品相互独立.
,且各件产品是否为优质品相互独立.
(1)求这批产品通过检验的概率;
(2)已知每件产品检验费用为100元,凡抽取的每件产品都需要检验,对这批产品作质量检验所需的费用记为X(单位:元),求X的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
图是某市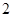 月
月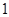 日至
日至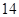 日的空气质量指数趋势图,空气质量指数(
日的空气质量指数趋势图,空气质量指数(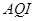 )小于
)小于 表示空气质量优良,空气质量指数大于
表示空气质量优良,空气质量指数大于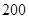 表示空气重度污染,某人随机选择
表示空气重度污染,某人随机选择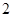 月
月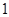 日至
日至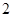 月
月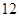 日中的某一天到达该市,并停留
日中的某一天到达该市,并停留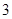 天.
天.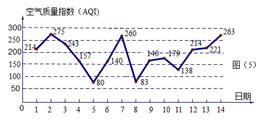
(1)求此人到达当日空气质量优良的概率;
(2)求此人停留期间至多有1天空气重度污染的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
年龄在60岁(含60岁)以上的人称为老龄人,某地区老龄人共有35万,随机调查了该地区700名老龄人的健康状况,结果如下表:
| 健康指数 | 2 | 1 | 0 | -1 |
| 60岁至79岁的人数 | 250 | 260 | 65 | 25 |
| 80岁及以上的人数 | 20 | 45 | 20 | 15 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某单位从一所学校招收某类特殊人才.对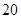 位已经选拔入围的学生进行运动协调能力和逻辑思维能力的测试,其测试结果如下表:
位已经选拔入围的学生进行运动协调能力和逻辑思维能力的测试,其测试结果如下表:
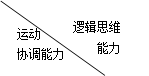 | 一般 | 良好 | 优秀 |
| 一般 |  |  |  |
| 良好 | 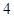 |  |  |
| 优秀 |  |  | 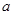 |
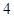 人.由于部分数据丢失,只知道从这
人.由于部分数据丢失,只知道从这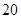 位参加测试的学生中随机抽取一位,抽到逻辑思维能力优秀的学生的概率为
位参加测试的学生中随机抽取一位,抽到逻辑思维能力优秀的学生的概率为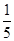 .
.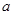 ,
, 的值;
的值; 位,求其中至少有一位逻辑思维能力优秀的学生的概率.
位,求其中至少有一位逻辑思维能力优秀的学生的概率.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知某种零件的尺寸X(单位:mm)服从正态分布,其正态曲线在(0,80)上是增函数,在(80,+∞)上是减函数,且f(80)= .
.
(1)求正态分布密度函数的解析式;
(2)估计尺寸在72mm~88mm之间的零件大约占总数的百分之几.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某大厦的一部电梯从底层出发后只能在第18,19,20层可以停靠,若该电梯在底层载有5位乘客,且每位乘客在这三层的每一层下电梯的概率均为 ,用X表示这5位乘客在第20层下电梯的人数,求随机变量X的分布列.
,用X表示这5位乘客在第20层下电梯的人数,求随机变量X的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,由M到N的电路中有4个元件,分别标为T1,T2,T3,T4,电流能通过T1,T2,T3的概率都是p,电流能通过T4的概率是0.9.电流能否通过各元件相互独立.已知T1,T2,T3中至少有一个能通过电流的概率为0.999.
(1)求p;
(2)求电流能在M与N之间通过的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
甲乙丙丁4人玩传球游戏,持球者将球等可能的传给其他3人,若球首先从甲传出,经过3次传球.
(1)求球恰好回到甲手中的概率;
(2)设乙获球(获得其他游戏者传的球)的次数为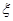 ,求
,求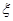 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com