
年龄在60岁(含60岁)以上的人称为老龄人,某地区老龄人共有35万,随机调查了该地区700名老龄人的健康状况,结果如下表:
| 健康指数 | 2 | 1 | 0 | -1 |
| 60岁至79岁的人数 | 250 | 260 | 65 | 25 |
| 80岁及以上的人数 | 20 | 45 | 20 | 15 |
(1) ;(2)不能.
;(2)不能.
解析试题分析:(1)该地区80岁以下老龄人生活能够自理的频率=80岁以下老龄人生活能够自理的人数÷80岁以下老龄人的总数,用频率估计概率即可;(2)分别求出 取值为
取值为 时的频率,进而列出对应的分布列,根据公式
时的频率,进而列出对应的分布列,根据公式 求出这个地区老龄人健康指数的平均值,再与1.2进行比较,从而判断这个地区是否能被评为“老龄健康地区”.
求出这个地区老龄人健康指数的平均值,再与1.2进行比较,从而判断这个地区是否能被评为“老龄健康地区”.
试题解析:(1)该地区80岁以下老龄人生活能够自理的频率为 ,
,
所以该地区80岁以下老龄人生活能够自理的概率约为 . 5分
. 5分
(2)该地区老龄人健康指数的 可能取值为
可能取值为 ,其分布列为(用频率估计概率):
,其分布列为(用频率估计概率):
 ,
,
因为 ,所以该地区不能被评为“老龄健康地区”. 13分
,所以该地区不能被评为“老龄健康地区”. 13分
考点:1.期望与方差;2.离散型随机变量的分布列;3.频率和概率


科目:高中数学 来源: 题型:解答题
低碳生活,从“衣食住行”开始.在国内一些网站中出现了“碳足迹”的应用,人们可以由此计算出自己每天的碳排放量,如家居用电的二氧化碳排放量(千克)=耗电度数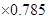 ,家用天然气的二氧化碳排放量(千克)=天然气使用立方数
,家用天然气的二氧化碳排放量(千克)=天然气使用立方数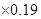 等.某校开展“节能减排,保护环境,从我做起!”的活动,该校高一、六班同学利用假期在东城、西城两个小区进行了逐户的关于“生活习惯是否符合低碳排放标准”的调查.生活习惯符合低碳观念的称为“低碳家庭”,否则称为“非低碳家庭”.经统计,这两类家庭占各自小区总户数的比例
等.某校开展“节能减排,保护环境,从我做起!”的活动,该校高一、六班同学利用假期在东城、西城两个小区进行了逐户的关于“生活习惯是否符合低碳排放标准”的调查.生活习惯符合低碳观念的称为“低碳家庭”,否则称为“非低碳家庭”.经统计,这两类家庭占各自小区总户数的比例 数据如下:
数据如下:
(1)如果在东城、西城两个小区内各随机选择2个家庭,求这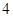 个家庭中恰好有两个家庭是“低碳家庭”的概率;
个家庭中恰好有两个家庭是“低碳家庭”的概率;
(2)该班同学在东城小区经过大力宣传节能减排的重要意义,每周“非低碳家庭”中有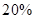 的家庭能加入到“低碳家庭”的行列中.宣传两周后随机地从东城小区中任选
的家庭能加入到“低碳家庭”的行列中.宣传两周后随机地从东城小区中任选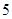 个家庭,记
个家庭,记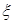 表示
表示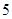 个家庭中“低碳家庭”的个数,求
个家庭中“低碳家庭”的个数,求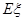 和
和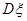 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
一个袋中装有形状大小完全相同的球9个,其中红球3个,白球6个,每次随机取1个,直到取出3次红球即停止.
(1)从袋中不放回地取球,求恰好取4次停止的概率P1;
(2)从袋中有放回地取球.
①求恰好取5次停止的概率P2;
②记5次之内(含5次)取到红球的个数为 ,求随机变量
,求随机变量 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
甲乙两个同学进行定点投篮游戏,已知他们每一次投篮投中的概率均为 ,且各次投篮的结果互不影响.甲同学决定投5次,乙同学决定投中1次就停止,否则就继续投下去,但投篮次数不超过5次.
,且各次投篮的结果互不影响.甲同学决定投5次,乙同学决定投中1次就停止,否则就继续投下去,但投篮次数不超过5次.
(1)求甲同学至少有4次投中的概率;
(2)求乙同学投篮次数 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
为了解甲、乙两个快递公司的工作状况,假设同一个公司快递员的工作状况基本相同,现从甲、乙两公司各随机抽取一名快递员,并从两人某月(30天)的快递件数记录结果中随机抽取10天的数据,制表如下:
| 甲公司某员工A | | 乙公司某员工B | ||||||||||||
| 3 | 9 | 6 | 5 | 8 | 3 | 3 | 2 | 3 | 4 | 6 | 6 | 6 | 7 | 7 |
| | | | | | | 0 | 1 | 4 | 4 | 2 | 2 | 2 | | |
 (单位:元),求
(单位:元),求 的分布列和数学期望;
的分布列和数学期望;查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知正方形ABCD的边长为2,E,F,G,H分别是边AB,BC,CD,DA的中点.
(1)从C,D,E,F,G,H这六个点中,随机选取两个点,记这两个点之间的距离的平方为 ,求概率P
,求概率P .
.
(2)在正方形ABCD内部随机取一点P,求满足 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知一个矩形由三个相同的小矩形拼凑而成(如图所示),用三种不同颜色给3个小矩形涂色,每个小矩形只涂一种颜色,求:
(1)3个矩形都涂同一颜色的概率;
(2)3个小矩形颜色都不同的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某地位于甲、乙两条河流的交汇处,根据统计资料预测,今年汛期甲河流发生洪水的概率为0.25,乙河流发生洪水的概率为0.18(假设两河流发生洪水与否互不影响).现有一台大型设备正在该地工作,为了保护设备,施工部门提出以下三种方案:
方案1:运走设备,此时需花费4000元;
方案2:建一保护围墙,需花费1000元,但围墙只能抵御一个河流发生的洪水,当两河流同时发生洪水时,设备仍将受损,损失约56000元;
方案3:不采取措施,此时,当两河流都发生洪水时损失达60000元,只有一条河流发生洪水时,损失为10000元.
(1)试求方案3中损失费X(随机变量)的分布列;
(2)试比较哪一种方案好.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
判断下列命题正确与否.
(1)先后掷两枚质地均匀的硬币,等可能出现“两个正面”“两个反面”“一正一反”三种结果;
(2)某袋中装有大小均匀的三个红球、两个黑球、一个白球,任取一球,那么每种颜色的球被摸到的可能性相同;
(3)从-4,-3,-2,-1,0,1,2中任取一数,取到的数小于0与不小于0的可能性相同;
(4)分别从3名男同学、4名女同学中各选一名代表,男、女同学当选的可能性相同.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com