
为了解甲、乙两个快递公司的工作状况,假设同一个公司快递员的工作状况基本相同,现从甲、乙两公司各随机抽取一名快递员,并从两人某月(30天)的快递件数记录结果中随机抽取10天的数据,制表如下:
| 甲公司某员工A | | 乙公司某员工B | ||||||||||||
| 3 | 9 | 6 | 5 | 8 | 3 | 3 | 2 | 3 | 4 | 6 | 6 | 6 | 7 | 7 |
| | | | | | | 0 | 1 | 4 | 4 | 2 | 2 | 2 | | |
 (单位:元),求
(单位:元),求 的分布列和数学期望;
的分布列和数学期望;(1)平均数为36,众数为33.(2)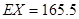
(3)甲公司4860元,乙公司4965元
136 147 154 189 203 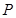
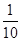
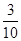
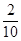
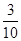
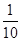
解析试题分析:(1)由平均数计算公式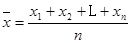 得:
得: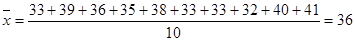 ,出现得最多的数是33.(2)先计算出随机变量取值集合,当投递件数为34时,
,出现得最多的数是33.(2)先计算出随机变量取值集合,当投递件数为34时,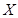 =136元;当投递件数为36时,
=136元;当投递件数为36时,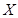 =147元;当投递件数为37时,
=147元;当投递件数为37时,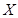 =154元;当投递件数为42时,
=154元;当投递件数为42时,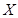 =189元;当投递件数为44时,
=189元;当投递件数为44时,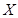 =1203元;再分别求出其概率,最后利用数学期望公式
=1203元;再分别求出其概率,最后利用数学期望公式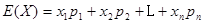 求出
求出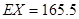 (3)甲公司被抽取员工该月收入为
(3)甲公司被抽取员工该月收入为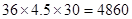 元,乙公司被抽取员工该月收入为
元,乙公司被抽取员工该月收入为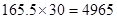 元.
元.
试题解析:解:
(1)甲公司员工A投递快递件数的平均数为36,众数为33. 2分
(2)设 为乙公司员工B投递件数,则
为乙公司员工B投递件数,则
当 =34时,
=34时,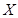 =136元,当
=136元,当 >35时,
>35时,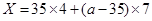 元,
元, 的可能取值为136,147,154,189,203 4分
的可能取值为136,147,154,189,203 4分
{说明:X取值都对给4分,若计算有错,在4分基础上错1个扣1分,4分扣完为止 的分布列为:
的分布列为:
9分
136 147 154 189 203 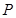
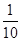
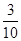
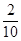
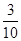
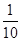
{说明:每个概率值给1分,不化简不扣分,随机变量值计算错误的此处不再重复扣分}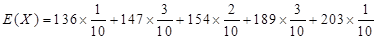
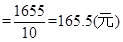 11分
11分
(3)根据图中数据,可估算甲公司被抽取员工该月收入4860元,乙公司被抽取员工该月收入4965元. 13分
考点:分布列,数学期望


科目:高中数学 来源: 题型:解答题
某校高三(1)班共有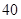 名学生,他们每天自主学习的时间全部在
名学生,他们每天自主学习的时间全部在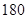 分钟到
分钟到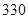 分钟之间,按他们学习时间的长短分
分钟之间,按他们学习时间的长短分 个组统计,得到如下频率分布表:
个组统计,得到如下频率分布表:
| 组别 | 分组 | 频数 | 频率 |
| 第一组 | 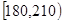 | | 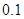 |
| 第二组 | 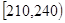 |  | 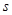 |
| 第三组 | 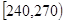 | 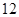 | 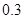 |
| 第四组 | 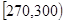 | 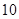 | 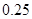 |
| 第五组 | 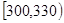 | | 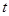 |
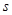 ,
,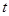 的值;
的值;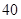 名学生中抽取
名学生中抽取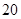 名进行研究,问应抽取多少名第一组的学生?
名进行研究,问应抽取多少名第一组的学生?查看答案和解析>>
科目:高中数学 来源: 题型:解答题
图是某市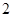 月
月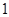 日至
日至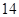 日的空气质量指数趋势图,空气质量指数(
日的空气质量指数趋势图,空气质量指数(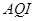 )小于
)小于 表示空气质量优良,空气质量指数大于
表示空气质量优良,空气质量指数大于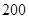 表示空气重度污染,某人随机选择
表示空气重度污染,某人随机选择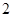 月
月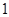 日至
日至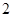 月
月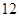 日中的某一天到达该市,并停留
日中的某一天到达该市,并停留 天.
天.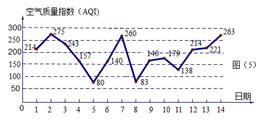
(1)求此人到达当日空气质量优良的概率;
(2)求此人停留期间至多有1天空气重度污染的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某校举行中学生“日常生活小常识”知识比赛,比赛分为初赛和复赛两部分,初赛采用选手从备选题中选一题答一题的方式进行;每位选手最多有5次答题机会,选手累计答对3题或答错3题即终止比赛,答对3题者直接进入复赛,答错3题者则被淘汰.已知选手甲答对每个题的概率均为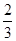 ,且相互间没有影响.
,且相互间没有影响.
(1)求选手甲进入复赛的概率;
(2)设选手甲在初赛中答题的个数为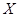 ,试求
,试求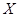 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
年龄在60岁(含60岁)以上的人称为老龄人,某地区老龄人共有35万,随机调查了该地区700名老龄人的健康状况,结果如下表:
| 健康指数 | 2 | 1 | 0 | -1 |
| 60岁至79岁的人数 | 250 | 260 | 65 | 25 |
| 80岁及以上的人数 | 20 | 45 | 20 | 15 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某单位从一所学校招收某类特殊人才.对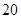 位已经选拔入围的学生进行运动协调能力和逻辑思维能力的测试,其测试结果如下表:
位已经选拔入围的学生进行运动协调能力和逻辑思维能力的测试,其测试结果如下表:
 | 一般 | 良好 | 优秀 |
| 一般 |  |  |  |
| 良好 | 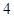 |  |  |
| 优秀 |  |  | 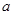 |
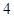 人.由于部分数据丢失,只知道从这
人.由于部分数据丢失,只知道从这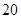 位参加测试的学生中随机抽取一位,抽到逻辑思维能力优秀的学生的概率为
位参加测试的学生中随机抽取一位,抽到逻辑思维能力优秀的学生的概率为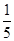 .
.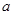 ,
, 的值;
的值; 位,求其中至少有一位逻辑思维能力优秀的学生的概率.
位,求其中至少有一位逻辑思维能力优秀的学生的概率.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某大厦的一部电梯从底层出发后只能在第18,19,20层可以停靠,若该电梯在底层载有5位乘客,且每位乘客在这三层的每一层下电梯的概率均为 ,用X表示这5位乘客在第20层下电梯的人数,求随机变量X的分布列.
,用X表示这5位乘客在第20层下电梯的人数,求随机变量X的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
全国第十二届全国人民代表大会第二次会议和政协第十二届全国委员会第二次会议,2014年3月在北京开幕.期间为了了解国企员工的工资收入状况,从108名相关人员中用分层抽样方法抽取若干人组成调研小组,有关数据见下表:(单位:人)
| | 相关人数 | 抽取人数 |
| 一般职工 | 63 | 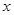 |
| 中层 | 27 | 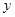 |
| 高管 | 18 | 2 |
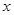 ,
,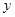 ;
;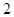 人,求这二人都来自中层的概率.
人,求这二人都来自中层的概率.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某工艺厂开发一种新工艺品,头两天试制中,该厂要求每位师傅每天制作10件,该厂质检部每天从每位师傅制作的10件产品中随机抽取4件进行检查,若发现有次品,则当天该师傅的产品不能通过.已知李师傅第一天、第二天制作的工艺品中分别有2件、1件次品.
(1)求两天中李师傅的产品全部通过检查的概率;
(2)若厂内对师傅们制作的工艺品采用记分制,两天全不通过检查得0分,通过1天、2天分别得1分、2分,求李师傅在这两天内得分的数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com