
已知正方形ABCD的边长为2,E,F,G,H分别是边AB,BC,CD,DA的中点.
(1)从C,D,E,F,G,H这六个点中,随机选取两个点,记这两个点之间的距离的平方为 ,求概率P
,求概率P .
.
(2)在正方形ABCD内部随机取一点P,求满足 的概率.
的概率.
(1)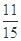 ;(2)
;(2) 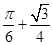
解析试题分析:(1)依题意由六个点中任取两个点共有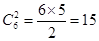 种情况,而其中两个点之间的距离的平方大于4的情况有4种,所以符合题意的共有11种,即可得到结论.本小题考查古典概型的问题,“正难则反”,也是这类题中的一种解题方法.
种情况,而其中两个点之间的距离的平方大于4的情况有4种,所以符合题意的共有11种,即可得到结论.本小题考查古典概型的问题,“正难则反”,也是这类题中的一种解题方法.
(2)因为正方形ABCD内部随机取一点P,则满足 的概率,即需要求出点P所围成的面积,通过求出一个扇形与两个直角三角形的面积和,即可求得结论.
的概率,即需要求出点P所围成的面积,通过求出一个扇形与两个直角三角形的面积和,即可求得结论.
试题解析:(1)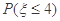 =
=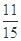
(2)这是一个几何概型.所有点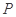 构成的平面区域是正方形
构成的平面区域是正方形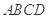 的内部,其面积是
的内部,其面积是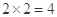 .满足
.满足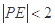 的点
的点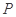 构成的平面区域是以
构成的平面区域是以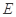 为圆心,2为半径的圆的内部与正方形
为圆心,2为半径的圆的内部与正方形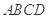 内部的公共部分,它可以看作是由一个以
内部的公共部分,它可以看作是由一个以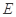 为圆心、2为半径、圆心角为
为圆心、2为半径、圆心角为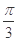 的扇形的内部与两个直角边分别为1和
的扇形的内部与两个直角边分别为1和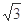 的直角三角形内部构成.其面积是
的直角三角形内部构成.其面积是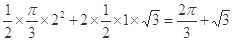 .
.
所以满足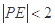 的概率为
的概率为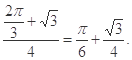
考点:1.古典概型的知识.2.几何概型的知识.3.正难则反推理的数学思想.


 优等生题库系列答案
优等生题库系列答案科目:高中数学 来源: 题型:解答题
设进入某商场的每一位顾客购买甲种商品的概率为0.5,购买乙种商品的概率为0.6,且购买甲种商品与购买乙种商品相互独立,各顾客之间购买商品也是相互独立的.
(1)求进入商场的1位顾客购买甲、乙两种商品中的一种的概率;
(2)求进入商场的1位顾客至少购买甲、乙两种商品中的一种的概率;
(3)记ξ表示进入商场的3位顾客中至少购买甲、乙两种商品中的一种的人数,求ξ的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
本着健康、低碳的生活理念,租自行车骑游的人越来越多.某自行车租车点的收费标准是每车每次租不超过两小时免费,超过两小时的收费标准为2元(不足1小时的部分按1小时计算).有人独立来该租车点则车骑游.各租一车一次.设甲、乙不超过两小时还车的概率分别为 ,
,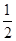 ;两小时以上且不超过三小时还车的概率分别为
;两小时以上且不超过三小时还车的概率分别为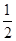 ,
, ;两人租车时间都不会超过四小时.
;两人租车时间都不会超过四小时.
(1)求出甲、乙所付租车费用相同的概率;
(2)求甲、乙两人所付的租车费用之和为随机变量X,求X的分布列与数学期望E(X).
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
一个袋中装有四个形状大小完全相同的球,球的编号分别为1,2,3,4.
(1)从袋中随机抽取两个球,求取出的球的编号之和不大于4的概率;
(2)先从袋中随机取一个球,该球的编号为m,将球放回袋中,然后再从袋中随机取一个球,该球的编号为n,求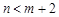 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
年龄在60岁(含60岁)以上的人称为老龄人,某地区老龄人共有35万,随机调查了该地区700名老龄人的健康状况,结果如下表:
| 健康指数 | 2 | 1 | 0 | -1 |
| 60岁至79岁的人数 | 250 | 260 | 65 | 25 |
| 80岁及以上的人数 | 20 | 45 | 20 | 15 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
甲、乙两药厂生产同一型号药品,在某次质量检测中,两厂各有5份样品送检,检测的平均得分相等(检测满分为100分,得分高低反映该样品综合质量的高低).成绩统计用茎叶图表示如下:
| 甲 | | 乙 |
| 9 8 | 8 | 4 8 9 |
| 2 1 0 | 9 |  6 6 |
 ;
;查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知某种零件的尺寸X(单位:mm)服从正态分布,其正态曲线在(0,80)上是增函数,在(80,+∞)上是减函数,且f(80)= .
.
(1)求正态分布密度函数的解析式;
(2)估计尺寸在72mm~88mm之间的零件大约占总数的百分之几.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
对一批共50件的某电器进行分类检测,其重量(克)统计如下:
| 重量段 | [80,85) | [85,90) | [90,95) | [95,100] |
| 件数 | 5 | a | 15 | b |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
江西某品牌豆腐食品是经过 、
、 、
、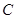 三道工序加工而成的,
三道工序加工而成的, 、
、 、
、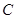 工序的产品合格率分别为
工序的产品合格率分别为 、
、 、
、 .已知每道工序的加工都相互独立,三道工序加工的产品都为合格时产品为一等品;恰有两次合格为二等品;其它的为废品,不进入市场.
.已知每道工序的加工都相互独立,三道工序加工的产品都为合格时产品为一等品;恰有两次合格为二等品;其它的为废品,不进入市场.
(1)生产一袋豆腐食品,求产品为废品的概率;
(2)生产一袋豆腐食品,设 为三道加工工序中产品合格的工序数,求
为三道加工工序中产品合格的工序数,求 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com