练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    设进入某商场的每一位顾客购买甲种商品的概率为0.5，购买乙种商品的概率为0.6，且购买甲种商品与购买乙种商品相互独立，各顾客之间购买商品也是相互独立的．
    (1)求进入商场的1位顾客购买甲、乙两种商品中的一种的概率；
    (2)求进入商场的1位顾客至少购买甲、乙两种商品中的一种的概率；
    (3)记ξ表示进入商场的3位顾客中至少购买甲、乙两种商品中的一种的人数，求ξ的分布列．

    （1）0.5（2）0.8（3）

    ξ
    		0
    		1
    		2
    		3
    P
    		0.008
    		0.096
    		0.384
    		0.512

    解析

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    如图，从参加环保知识竞赛的学生中抽出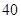名，将其成绩（均为整数）整理后画出的频率分布直方图如下：观察图形，回答下列问题：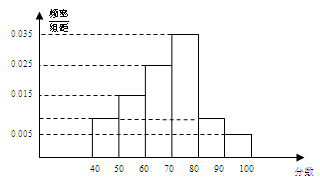

    （1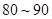）这一组的频数、频率分别是多少？
    （2）估计这次环保知识竞赛成绩的平均数、众数、中位数。（不要求写过程）
    (3) 从成绩是80分以上（包括80分）的学生中选两人，求他们在同一分数段的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    下图是某市3月1日至14日空气质量指数趋势图，空气质量指数小于1 00表示空气质量优良，空气质量指数大于200表示空气重度污染，某人随机选择3月1曰至3月1 3日中某一天到达该市，并停留2天．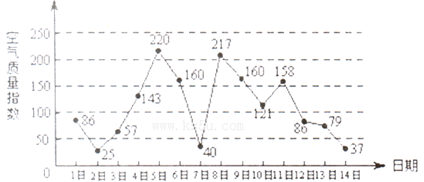

    (l)求此人到达当日空气重度污染的概率；
    (2)设X是此人停留期间空气质量优良的天数，求X的分布列与数学期望。

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    低碳生活，从“衣食住行”开始．在国内一些网站中出现了“碳足迹”的应用，人们可以由此计算出自己每天的碳排放量，如家居用电的二氧化碳排放量（千克）＝耗电度数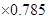，家用天然气的二氧化碳排放量（千克）＝天然气使用立方数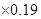等．某校开展“节能减排，保护环境，从我做起！”的活动，该校高一、六班同学利用假期在东城、西城两个小区进行了逐户的关于“生活习惯是否符合低碳排放标准”的调查．生活习惯符合低碳观念的称为“低碳家庭”，否则称为“非低碳家庭”．经统计，这两类家庭占各自小区总户数的比例数据如下：

    （1）如果在东城、西城两个小区内各随机选择2个家庭，求这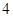个家庭中恰好有两个家庭是“低碳家庭”的概率；
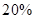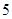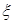    （2）该班同学在东城小区经过大力宣传节能减排的重要意义，每周“非低碳家庭”中有的家庭能加入到“低碳家庭”的行列中．宣传两周后随机地从东城小区中任选个家庭，记表示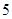个家庭中“低碳家庭”的个数，求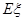和．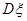

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    为防止山体滑坡，某地决定建设既美化又防护的绿化带，种植松树、柳树等植物．某人一次种植了n株柳树，各株柳树成活与否是相互独立的，成活率为p，设ξ为成活柳树的株数，数学期望E(ξ)＝3，标准差σ(ξ)为.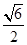
    (1)求n、p的值并写出ξ的分布列；
    (2)若有3株或3株以上的柳树未成活，则需要补种，求需要补种柳树的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    甲、乙两支排球队进行比赛，约定先胜3局者获得比赛的胜利，比赛随即结束，除第五局甲队获胜的概率是外，其余每局比赛甲队获胜的概率都是，假设各局比赛结果相互独立．
    (1)分别求甲队以3∶0，3∶1，3∶2胜利的概率；
    (2)若比赛结果为3∶0或3∶1，则胜利方得3分，对方得0分；若比赛结果为3∶2，则胜利方得2分、对方得1分．求乙队得分X的分布列．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    现有甲、乙、丙三人参加某电视台的应聘节目《非你莫属》，若甲应聘成功的概率为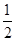，乙、丙应聘成功的概率均为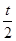，（0<t<2），且三个人是否应聘成功是相互独立的.
    （1）若乙、丙有且只有一个人应聘成功的概率等于甲应聘成功的概率，求t的值；
    （2）记应聘成功的人数为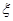，若当且仅当为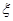=2时概率最大，求E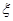（）的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知正方形ABCD的边长为2，E,F,G,H分别是边AB,BC,CD,DA的中点.
    （1）从C,D,E,F,G,H这六个点中，随机选取两个点，记这两个点之间的距离的平方为，求概率P.
    (2)在正方形ABCD内部随机取一点P，求满足的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知离散型随机变量ξ1的概率分布为

    ξ1
    		1
    		2
    		3
    		4
    		5
    		6
    		7
    P







    离散型随机变量ξ2的概率分布为
    ξ2
    		3.7
    		3.8
    		3.9
    		4
    		4.1
    		4.2
    		4.3
    P







    求这两个随机变量数学期望、方差与标准差．

    查看答案和解析>>

    同步练习册答案