
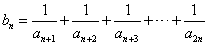 ����������������n����m��[-1��1]ʱ������ʽt2-mt+
����������������n����m��[-1��1]ʱ������ʽt2-mt+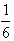 ��bn���������ʵ��t��ȡֵ��Χ��
��bn���������ʵ��t��ȡֵ��Χ��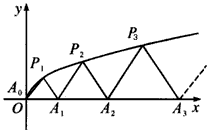
�⣺(1)a1=2��a2=6��a3=12��
(2)������An(an��0)��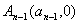 ��
��
�� ��
��
����������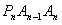 ����
����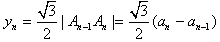 ��
��
�� ��
��
��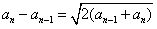 ��
��
��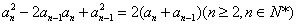 ����
����
ͬ���ɵ�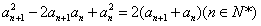 ����
����
��-�ٲ����ε�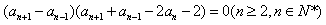 ��
��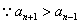 ��
��
�� ��
��
��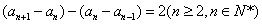 ��
��
������{an+1-an}����a2-a1=4Ϊ�������Ϊ2�ĵȲ����У�
�� ��
��
��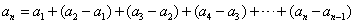
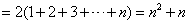 ��
��
��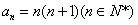 ��
��
(3)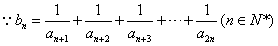 ��
��
��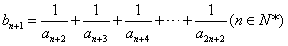 ��
��
��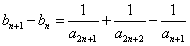
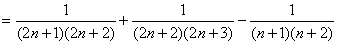
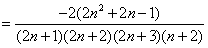 ��
��
�ߵ�n��N*ʱ����ʽ��Ϊ��ֵ��
�൱n��N*ʱ��bn+1��bn��
������{bn}�ǵݼ����У�
��bn�����ֵΪ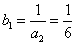 ��
��
��������������n����m��[-1��1]ʱ������ʽ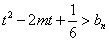 �������
�������
��ʽ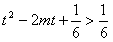 ��m��[-1��1]ʱ�������
��m��[-1��1]ʱ�������
������ʽt2-2mt��0��m��[-1��1]ʱ�������
��f(m)=t2-2mt����f(1)��0��f(-1)��0��
��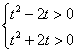 ����֮����t��-2��t��2��
����֮����t��-2��t��2��
��t��ȡֵ��Χ��(-�ޣ�-2)��(2��+��)��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
| 1 |
| an+1 |
| 1 |
| an+2 |
| 1 |
| an+3 |
| 1 |
| a2n |
| 1 |
| 6 |

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
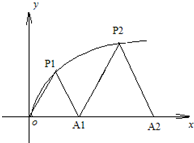 ��ͼ��P1��x1��y1����P2��x2��y2��������Pn��xn��yn����0��y1��y2������yn�� ������C��y2=3x��y��0���ϵ�n���㣬��Ai��ai��0����i=1��2��3����n����x����������ϣ��ҡ�Ai-1AiPi���������Σ�A0������ԭ�㣩��
��ͼ��P1��x1��y1����P2��x2��y2��������Pn��xn��yn����0��y1��y2������yn�� ������C��y2=3x��y��0���ϵ�n���㣬��Ai��ai��0����i=1��2��3����n����x����������ϣ��ҡ�Ai-1AiPi���������Σ�A0������ԭ�㣩���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��2012•բ������ģ����ͼ��P1��x1��y1����P2��x2��y2��������Pn��xn��yn������������C��y2=
��2012•բ������ģ����ͼ��P1��x1��y1����P2��x2��y2��������Pn��xn��yn������������C��y2=| 1 |
| 2 |
| 1 |
| an+1 |
| 1 |
| an+2 |
| 1 |
| an+3 |
| 1 |
| a2n |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��2012•բ������ģ����ͼ��P1��x1��y1����P2��x2��y2��������Pn��xn��yn������������C��y2=
��2012•բ������ģ����ͼ��P1��x1��y1����P2��x2��y2��������Pn��xn��yn������������C��y2=| 1 |
| 2 |
| n(n+1) |
| 2 |
| 1 |
| an+1 |
| 1 |
| an+2 |
| 1 |
| an+3 |
| 1 |
| a2n |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com