
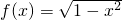 ,若直线y=2x+m与函数图象始终相交,则实数m的取值范围________.
,若直线y=2x+m与函数图象始终相交,则实数m的取值范围________. ]
]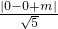 求得 m的值.当直线y=2x+m过点A(1,0)时,求得m的值,数形结合可得
求得 m的值.当直线y=2x+m过点A(1,0)时,求得m的值,数形结合可得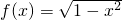 ,可得 x2+y2=1 (y≥0),表示一个以原点O为圆心,半径等于1的位于x轴及x轴上方的半圆,如图所示:
,可得 x2+y2=1 (y≥0),表示一个以原点O为圆心,半径等于1的位于x轴及x轴上方的半圆,如图所示: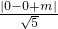 求得 m=
求得 m= ,或 m=-
,或 m=- (舍去).
(舍去). ],
], ].
].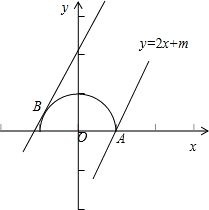


 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:高中数学 来源:福建省福州三中2012届高三校模拟数学文科试题 题型:044
已知函数![]()
(1)若曲线y=f(x)在点P(1,f(1))处的切线与直线y=x+2垂直,求函数y=f(x)的单调区间;
(2)若对![]() ,都有
,都有![]() 恒成立,试求实数a的取值范围;
恒成立,试求实数a的取值范围;
(3)记g(x)=f(x)+x-b,当a=1时,函数g(x)在区间[e-1,e]上有两个零点,求实数b的取值范围(e为自然对数的底数).
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)是y=![]() -1(x∈R)的反函数,函数g(x)的图像
-1(x∈R)的反函数,函数g(x)的图像
与函数y=-![]() 的图像关于y轴对称,设F(x)=f(x)+g(x).
的图像关于y轴对称,设F(x)=f(x)+g(x).
(1)求函数F(x)的解析式及定义域;
(2)试问在函数F(x)的图像上是否存在两个不同的点A、B,使直线AB恰好与y轴垂直?若存在,求出A、B的坐标;若不存在,说明理由![]()
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
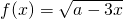 的反函数为y=f-1(x)
的反函数为y=f-1(x)查看答案和解析>>
科目:高中数学 来源:2012-2013学年上海外国语大学附中高三(上)第一次周练数学试卷(解析版) 题型:解答题
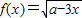 的反函数为y=f-1(x)
的反函数为y=f-1(x)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com