练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    △ABC中，已知其面积为S=
    1
    4
    (a2+b2-c2)    ，则角C的度数为（　　）
    分析：利用三角形面积公式表示出S，利用余弦定理表示出cosC，变形后都代入已知等式，利用同角三角函数间的基本关系化简求出tanC的值，即可确定出C的度数．
    解答：解：∵cosC=
    a2+b2-c2
    2ab
    ，即a2+b2-c2=2abcosC，S=
    1
    2
    absinC，且S=
    1
    4
    （a2+b2-c2），
    ∴
    1
    2
    absinC=
    1
    2
    abcosC，即tanC=1，
    ∵C为三角形的内角，
    ∴C=45°．
    故选B
    点评：此题考查了余弦定理，以及三角形的面积公式，熟练掌握余弦定理是解本题的关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2013届黑龙江省大庆铁人中学高三第三次阶段理科数学试卷（带解析） 题型：填空题

    下列四个命题：
    ①直线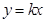与圆恒有公共点；
    ②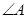为△ABC的内角，则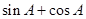最小值为；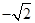
    ③已知a，b是两条异面直线，则过空间任意一点P都能作并且只能作一条直线与a，b都垂直；
    ④等差数列{}中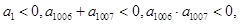，则使其前n项和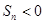成立的最大正整数为2013;
    其中正确命题的序号为               。（将你认为正确的命题的序号都填上）

    查看答案和解析>>

    科目：高中数学 来源：2013届山西省太原市第五中学高三4月月考文科数学试卷（带解析） 题型：填空题

    下列四个命题：
    ①直线与圆恒有公共点；
    ②为△ABC的内角，则最小值为；
    ③已知a，b是两条异面直线，则过空间任意一点P都能作并且只能作一条直线与a，b都垂直；
    ④等差数列{}中，则使其前n项和成立的最大正整数为2013;
    其中正确命题的序号为           。（将你认为正确的命题的序号都填上）

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年山西省太原市高三4月月考文科数学试卷（解析版） 题型：填空题

    下列四个命题：

    ①直线与圆恒有公共点；

    ②为△ABC的内角，则最小值为；

    ③已知a，b是两条异面直线，则过空间任意一点P都能作并且只能作一条直线与a，b都垂直；

    ④等差数列{}中，则使其前n项和成立的最大正整数为2013;

    其中正确命题的序号为           。（将你认为正确的命题的序号都填上）

     

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年黑龙江省高三第三次阶段理科数学试卷（解析版） 题型：填空题

    下列四个命题：

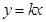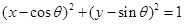    ①直线与圆恒有公共点；

    ②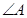为△ABC的内角，则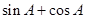最小值为；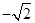

    ③已知a，b是两条异面直线，则过空间任意一点P都能作并且只能作一条直线与a，b都垂直；

    ④等差数列{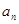}中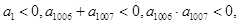，则使其前n项和成立的最大正整数为2013;

    其中正确命题的序号为               。（将你认为正确的命题的序号都填上）

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    (理)如图a所示，某地为了开发旅游资源，欲修建一条连接风景点P和居民区O的公路，点P所在的山坡面与山脚所在水平面α所成的二面角为θ(0°＜θ＜90°)，且sinθ=，点P到平面α的距离PH=0．4(km)．沿山脚原有一段笔直的公路AB可供利用．从点O到山脚修路的造价为a万元／km，原有公路改建费用为万元／km．当山坡上公路长度为l km(1≤l≤2)时，其造价为(l2+1)a万元已知OA⊥AB，PB⊥AB，AB=1．5(km)，OA=(km)．

    (1)在AB上求一点D，使沿折线PDAO修建公路的总造价最小；

    (2)对于(1)中得到的点D，在DA上求一点E，使沿折线PDEO修建公路的总造价最小；

    (3)在AB上是否存在两个不同的点D′，E′，使沿折线．PD′E′O修建公路的总造价小于(2)中得到的最小总造价?证明你的结论．

    a)

    第19题图

    (文)如图b所示，直四棱柱ABCD-A1B1C1D1中，∠ADC=90°，△ABC为等边三角形，且AA1=AD=DC=2．

    (1)求AC1与BC所成角的余弦值；

    (2)求二面角C1-BD-C的大小；

    (3)设M是BD上的点，当DM为何值时，D1M⊥平面A1C1D?并证明你的结论．

    第19题图

    查看答案和解析>>

    同步练习册答案