
已知函数f(x)=x2+2alnx.
(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)若函数 在
在 上是减函数,求实数a的取值范围.
上是减函数,求实数a的取值范围.
(Ⅰ)当a≥0时,递增区间为(0,+∞);当a<0时,递减区间是(0, );递增区间是(
);递增区间是( ,+∞);(Ⅱ)
,+∞);(Ⅱ) .
.
【解析】
试题分析:
解题思路:(Ⅰ)求定义域与导函数,因含有参数 ,分类讨论求出函数的单调区间;(Ⅱ)利用“函数g(x)为[1,2]上的单调减函数,则g′(x)≤0在[1,2]上恒成立”,得到不等式恒成立;再分离参数,求函数的最值即可.
,分类讨论求出函数的单调区间;(Ⅱ)利用“函数g(x)为[1,2]上的单调减函数,则g′(x)≤0在[1,2]上恒成立”,得到不等式恒成立;再分离参数,求函数的最值即可.
规律总结:若函数 在某区间上单调递增,则
在某区间上单调递增,则 在该区间恒成立;“若函数
在该区间恒成立;“若函数 在某区间上单调递减,则
在某区间上单调递减,则 在该区间恒成立.
在该区间恒成立.
试题解析:(Ⅰ)f′(x)=2x+ =
= , 函数f(x)的定义域为(0,+∞).
, 函数f(x)的定义域为(0,+∞).
①当a≥0时,f′(x)>0,f(x)的单调递增区间为(0,+∞);
②当a<0时,f′(x)= .
.
当x变化时,f′(x),f(x)的变化情况如下:
x | (0, |
| ( |
f′(x) | - | 0 | + |
f(x) |
| 极小值 |
|
由上表可知,函数f(x)的单调递减区间是(0, );单调递增区间是(
);单调递增区间是( ,+∞).
,+∞).
(Ⅱ)由g(x)=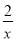 +x2+2aln x,得g′(x)=-
+x2+2aln x,得g′(x)=- +2x+
+2x+ ,
,
由已知函数g(x)为[1,2]上的单调减函数,则g′(x)≤0在[1,2]上恒成立,
即- +2x+
+2x+ ≤0在[1,2]上恒成立.即a≤
≤0在[1,2]上恒成立.即a≤ -x2在[1,2]上恒成立.
-x2在[1,2]上恒成立.
令h(x)= -x2,在[1,2]上h′(x)=-
-x2,在[1,2]上h′(x)=- -2x=-(
-2x=-( +2x)<0,
+2x)<0,
所以h(x)在[1,2]上为减函数,h(x)min=h(2)=- ,所以a≤-
,所以a≤- .
.
故实数a的取值范围为{a|a≤- }.
}.
考点:1.利用导数求函数的单调区间;2.根据函数的单调性求参数.


 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:高中数学 来源:2015届山东省高二暑假作业数学试卷三(解析版) 题型:解答题
已知函数 (
( ,
, )在一个周期上的一系列对应值如下表:
)在一个周期上的一系列对应值如下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(Ⅰ)求 的解析式;
的解析式;
(Ⅱ)在△ 中,
中, ,
, 为锐角,且
为锐角,且 ,求△
,求△ 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源:2015届山东省高二暑假作业二数学试卷(解析版) 题型:选择题
在下列区间中,函数f(x)=ex+4x-3的零点所在的区间( )
A.(-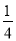 ,0) B.(0,
,0) B.(0, ) C.(
) C.( ,
, ) D.(
) D.( ,
, )
)
查看答案和解析>>
科目:高中数学 来源:2015届山东省菏泽市高二下学期期末考试理科数学试卷(解析版) 题型:填空题
如果随机变量ξ~B(n,p),且Eξ=7,Dξ=6,则P等于 _________ .
查看答案和解析>>
科目:高中数学 来源:2015届山东省菏泽市高二下学期期末考试理科数学试卷(解析版) 题型:选择题
直线y=4x与曲线y=x3在第一象限内围成的封闭图形的面积为( ).
A.2 B.4
B.4 C.2 D.4
C.2 D.4
查看答案和解析>>
科目:高中数学 来源:2015届山东省菏泽市高二下学期期末考试文科数学试卷(解析版) 题型:解答题
已知复数z=1﹣i(i是虚数单位)
(Ⅰ)计算z2;
(Ⅱ)若z2+a ,求实数a,b的值.
,求实数a,b的值.
查看答案和解析>>
科目:高中数学 来源:2015届山东省菏泽市高二下学期期末考试文科数学试卷(解析版) 题型:选择题
下列说法:
①将一组数据中的每个数据都加上或减去同一个常数后,方差恒不变;
②设有一个回归方程 ,变量x增加一个单位时,y平均增加5个单位;
,变量x增加一个单位时,y平均增加5个单位;
③线性回归方程 必过(
必过( );
);
④在一个2×2列联中,由计算得K2=13.079则有99%的把握确认这两个变量间有关系;
其中错误 的个数是( ).
本题可以参考独立性检验临界值表:
P(K2≥k) | 0.5 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.25 | 0.010 | 0.005 | 0.001 |
k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.535 | 7.879 | 10.828 |
A.0 B.1 C.2 D.3
查看答案和解析>>
科目:高中数学 来源:2015届山东省潍坊市高二下学期入学考试数学试卷(解析版) 题型:填空题
已知等比数列 的各项均为不等于1的正数,数列
的各项均为不等于1的正数,数列 满足
满足 ,
, =18,
=18, =12,则数列
=12,则数列 前n项和的最大值为________.
前n项和的最大值为________.
查看答案和解析>>
科目:高中数学 来源:2015届山东省高二下学期期中考试文科数学试卷(解析版) 题型:填空题
将函数 (ω>0)的图像向左平移
(ω>0)的图像向左平移 个单位,得到函数y=g(x)的图象.
个单位,得到函数y=g(x)的图象.
若y=g(x)在 上为增函数,则ω的最大值为________.
上为增函数,则ω的最大值为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com