
分析 (Ⅰ)由已知得an+1=3an.从而{an}是公比为3,首项为9的等比数列,由此能求出数列{an}的通项公式.
(Ⅱ)求出Sn=-$\frac{9}{2}$+$\frac{9}{2}$-3n,从而${S}_{n}+\frac{9}{2}$=$\frac{9}{2}$•3n=$\frac{27}{2}•{3}^{n-1}$,由此能证明数列{${S}_{n}+\frac{9}{2}$}是以$\frac{27}{2}$为首项,公比为3的等比数列.
解答 解:(Ⅰ)∵Sn=3(Sn-1+3),∴Sn+1=3(Sn+3),
∴an+1=3an.故{an}是公比为3,首项为9的等比数列,
∴an=3n+1.---(5分)
证明:(Ⅱ)因为${a}_{n}=9•{3}^{n-1}$,所以Sn=$\frac{9(1-{3}^{n})}{1-3}$=-$\frac{9}{2}$+$\frac{9}{2}$-3n,(7分)
所以,${S}_{n}+\frac{9}{2}$=$\frac{9}{2}$•3n=$\frac{27}{2}•{3}^{n-1}$,(9分)
${S}_{1}+\frac{9}{2}$=$\frac{9}{2}•3$=$\frac{27}{2}$,$\frac{{S}_{n+1}+\frac{9}{2}}{{S}_{n}+\frac{9}{2}}$=$\frac{\frac{27}{2}•{3}^{n}}{\frac{27}{2}•{3}^{n-1}}$=3.(10分)
故,数列{${S}_{n}+\frac{9}{2}$}是以$\frac{27}{2}$为首项,公比为3的等比数列.(12分)
点评 本题考查数列的通项公式的求法,考查等比数列的证明,是中档题,解题时要认真审题,注意等比数列的性质的合理运用.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | ($\frac{1}{2}$)${\;}^{\frac{2}{3}}$<($\frac{1}{5}$)${\;}^{\frac{2}{3}}$<($\frac{1}{2}$)${\;}^{\frac{1}{3}}$ | B. | ($\frac{1}{2}$)${\;}^{\frac{1}{3}}$>($\frac{1}{2}$)${\;}^{\frac{2}{3}}$>($\frac{1}{5}$)${\;}^{\frac{2}{3}}$ | ||
| C. | ($\frac{1}{2}$)${\;}^{\frac{1}{3}}$<($\frac{1}{2}$)${\;}^{\frac{2}{3}}$<($\frac{1}{5}$)${\;}^{\frac{2}{3}}$ | D. | ($\frac{1}{2}$)${\;}^{\frac{2}{3}}$><($\frac{1}{5}$)${\;}^{\frac{2}{3}}$>($\frac{1}{2}$)${\;}^{\frac{1}{3}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
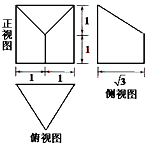
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{9}$ | B. | $\frac{5}{9}$ | C. | $\frac{25}{36}$ | D. | $\frac{11}{36}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
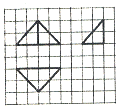
| A. | 8+4$\sqrt{3}$ | B. | 8+4$\sqrt{2}$ | C. | 8+16$\sqrt{2}$ | D. | 8+8$\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com