
【题目】已知函数f(x)=mln(x+1)﹣nx在点(1,f(1))处的切线与y轴垂直,且 ![]() ,其中 m,n∈R.
,其中 m,n∈R.
(Ⅰ)求m,n的值,并求出f(x)的单调区间;
(Ⅱ)设g(x)=﹣x2+2x,确定非负实数a的取值范围,使不等式f(x)+x≥ag(x)在[0,+∞)上恒成立.
【答案】解:(Ⅰ)对f(x)求导,得 ![]() ,
,
若f(x)在点(1,f(1))处的切线与y轴垂直,
则 ![]() ,又
,又 ![]() ,则
,则 ![]() ,
,
由 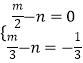 ,求得
,求得 ![]() ,
,
所以f(x)=2ln(x+1)﹣x,定义域为(﹣1,+∞),
对f(x)求导,得 ![]() ,
,
由f'(x)>0,求得﹣1<x<1,即f(x)的单调递增区间为(﹣1,1);
由f'(x)<0,求得x>1,即f(x)的单调递减区间为(1,+∞).
(Ⅱ)由(Ⅰ)知,不等式f(x)+x≥ag(x)即是2ln(x+1)≥a(﹣x2+2x),
于是问题可转化为不等式2ln(x+1)﹣a(﹣x2+2x)≥0在[0,+∞)上恒成立时,确定非负实数a的取值范围,
记h(x)=2ln(x+1)﹣a(﹣x2+2x),则 ![]() ,
,
① 当a=0时,对 ![]() ,则h(x)在[0,+∞)上为增函数,
,则h(x)在[0,+∞)上为增函数,
②当a>0时,令h'(x)=0,则ax2+1﹣a=0,当1﹣a≥0,
即0<a≤1时,对x≥0,h'(x)>0,则h(x)在[0,+∞)上为增函数,
所以h(x)=h(0)=0,此时命题成立;
当1﹣a<0,即a>1时,由ax2+1﹣a=0,
求得 ![]() .h(x),h'(x)的变化情况如表:
.h(x),h'(x)的变化情况如表:
x | 0 | (0,x2) | x2 | (x2 , +∞) |
h'(x) | ﹣ | 0 | + | |
h(x) | ↘ | 极小值 | ↗ |
因为h(x)min=h(x2)<h(0)=0,
所以当x≥0时,命题不成立
【解析】(Ⅰ)求出函数的导数,得到关于m,n的方程组,求出m,n的值,从而求出f(x)的导数,解关于导函数的不等式,求出函数的单调区间即可;(Ⅱ)问题可转化为不等式2ln(x+1)﹣a(﹣x2+2x)≥0在[0,+∞)上恒成立时,确定非负实数a的取值范围,记h(x)=2ln(x+1)﹣a(﹣x2+2x),根据函数的单调性求出a的范围即可.
【考点精析】根据题目的已知条件,利用利用导数研究函数的单调性的相关知识可以得到问题的答案,需要掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减.
在这个区间单调递减.


 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的首项为a1 , 公差为d,其前n项和为Sn , 若直线y=a1x+m与圆x2+(y﹣1)2=1的两个交点关于直线x+y﹣d=0对称,则数列( ![]() )的前100项的和为 .
)的前100项的和为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x﹣alnx,g(x)=﹣ ![]() ,其中a∈R
,其中a∈R
(1)设函数h(x)=f(x)﹣g(x),求函数h(x)的单调区间;
(2)若存在x0∈[1,e],使得f(x0)<g(x0)成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题正确的是( )
A.?x0∈R,sinx0+cosx0= ![]()
B.?x≥0且x∈R,2x>x2
C.已知a,b为实数,则a>2,b>2是ab>4的充分条件
D.已知a,b为实数,则a+b=0的充要条件是 ![]() =﹣1
=﹣1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在R上的函数f(x),当x∈[0,2]时,f(x)=4(1﹣|x﹣1|),且对于任意实数x∈[2n﹣2,2n+1﹣2](n∈N* , n≥2),都有f(x)= ![]() f(
f( ![]() ﹣1).若g(x)=f(x)﹣logax有且只有三个零点,则a的取值范围是( )
﹣1).若g(x)=f(x)﹣logax有且只有三个零点,则a的取值范围是( )
A.[2,10]
B.[ ![]() ,
, ![]() ]
]
C.(2,10)
D.[2,10)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个简单几何体的正视图、侧视图如图所示,则其俯视图可能是( )
①长、宽不相等的长方形 ②正方形 ③圆 ④椭圆.
A.①②
B.①④
C.②③
D.③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com