Question

【题目】已知函数f（x）= （a∈R），曲线y=f（x）在点（1，f（1））处的切线与直线x+y+1=0垂直． （Ⅰ）试比较20162017与20172016的大小，并说明理由；
（Ⅱ）若函数g（x）=f（x）﹣k有两个不同的零点x1 ， x2 ， 证明：x1x2＞e2 ．

Answer 1

【答案】解：（Ⅰ）函数f（x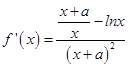）= ， ， 所以 ，又由切线与直线x+y+1=0垂直，
可得f′（1）=1，即 ，解得a=0．
此时 ， ，
令f'（x）＞0，即1﹣lnx＞0，解得0＜x＜e；
令f'（x）＜0，即1﹣lnx＜0，解得x＞e，
所以f（x）的增区间为（0，e），减区间为（e，+∞）．
所以f＞f，
即 ．
2017ln2016＞2016ln2017，即有20162017＞20172016 ．
（Ⅱ）证明：不妨设x1＞x2＞0，因为g（x1）=g（x2）=0，
所以化简得lnx1﹣kx1=0，lnx2﹣kx2=0．
可得lnx1+lnx2=k（x1+x2），lnx1﹣lnx2=k（x1﹣x2），
要证明， ，即证明lnx1+lnx2＞2，也就是k（x1+x2）＞2．
因为 ，即证 ，
即ln ＞ ，令 ，则t＞1，即证 ．
令 （t＞1）．
由 = ，
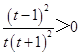故函数h（t）在（1，+∞）是增函数，
所以h（t）＞h（1）=0，即 得证．
所以 ．
【解析】（Ⅰ）求出f（x）的导数，由两直线垂直的条件：斜率相等，即可得到切线的斜率和切点坐标，进而f（x）的解析式和导数，求出单调区间，可得f＞f，即可得到20162017与20172016的大小；（Ⅱ）运用分析法证明，不妨设x1＞x2＞0，由根的定义可得所以化简得lnx1﹣kx1=0，lnx2﹣kx2=0．可得lnx1+lnx2=k（x1+x2），lnx1﹣lnx2=k（x1﹣x2），要证明， ，即证明lnx1+lnx2＞2，也就是k（x1+x2）＞2．求出k，即证 ，令 ，则t＞1，即证 ．令 （t＞1）．求出导数，判断单调性，即可得证．
【考点精析】掌握利用导数研究函数的单调性是解答本题的根本，需要知道一般的,函数的单调性与其导数的正负有如下关系： 在某个区间内，(1)如果，那么函数在这个区间单调递增；(2)如果，那么函数在这个区间单调递减．