
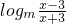
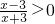 得f(x)的定义域为(-∞,-3)∪(3,+∞),关于原点对称.
得f(x)的定义域为(-∞,-3)∪(3,+∞),关于原点对称.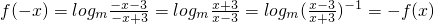
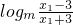
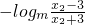 =
=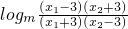
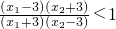 ,
,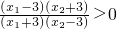 ,即f(x1)>f(x2);
,即f(x1)>f(x2);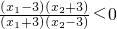 ,即f(x1)<f(x2),
,即f(x1)<f(x2),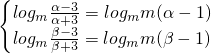 …(9分)
…(9分)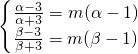
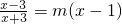 的两个解…(10分)
的两个解…(10分)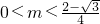 时,[α,β]=
时,[α,β]=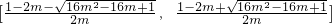 ,
,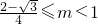 时,方程组无解,即[α,β]不存在. …(12分)
时,方程组无解,即[α,β]不存在. …(12分)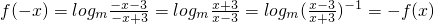 ,从而可得f(x)为奇函数;
,从而可得f(x)为奇函数;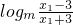
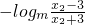 =
=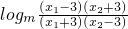 ,从而可知当0<m<1时,logm
,从而可知当0<m<1时,logm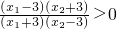 ,即f(x1)>f(x2);当m>1时,logm
,即f(x1)>f(x2);当m>1时,logm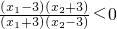 ,即f(x1)<f(x2),
,即f(x1)<f(x2),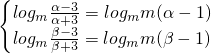 ,从而问题可转化为α,β是方程
,从而问题可转化为α,β是方程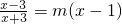 的两个解,进而问题得解.
的两个解,进而问题得解.

 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:高中数学 来源:2011-2012学年江苏省盐城市田家炳中学高三(上)期中数学试卷(解析版) 题型:解答题

 },B=[0,1],试判断A与B的关系;
},B=[0,1],试判断A与B的关系;查看答案和解析>>
科目:高中数学 来源:2012-2013学年湖南省五市十校高三第一次联考数学试卷(理科)(解析版) 题型:解答题

 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com