
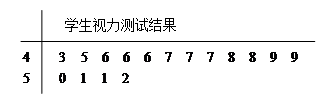
 表示抽到“好视力”学生的人数,求
表示抽到“好视力”学生的人数,求 的分布列及数学期望.
的分布列及数学期望.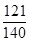 ;(2)分布列为
;(2)分布列为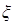 |  | 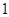 | 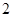 | 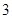 |
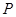 | 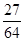 | 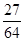 | 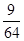 | 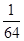 |
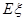
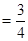 .
. 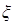 的所有可能取值为0、1、2、3,既然是以以这16人的样本数据来估计该市所有参加高考学生的的总体数据,则从该市参加高考的学生中任选1人是“好视力”学生的概率为
的所有可能取值为0、1、2、3,既然是以以这16人的样本数据来估计该市所有参加高考学生的的总体数据,则从该市参加高考的学生中任选1人是“好视力”学生的概率为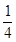 ,不是“好视力”学生的概率为
,不是“好视力”学生的概率为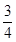 ,抽3人就是将“每次抽1人”的试验重复做三次,所以
,抽3人就是将“每次抽1人”的试验重复做三次,所以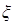 服从参数为3和
服从参数为3和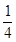 的二项分布,由n次独立重复试验恰有k次发生的概率公式
的二项分布,由n次独立重复试验恰有k次发生的概率公式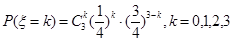 可求得
可求得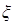 的分布列,进而可求得其数学期望.
的分布列,进而可求得其数学期望.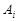 表示所取3人中有
表示所取3人中有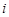 个人是“好视力”,至多有1人是“好视力”记为事件
个人是“好视力”,至多有1人是“好视力”记为事件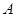 ,
,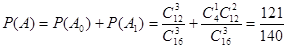 6分
6分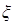 的可能取值为0、1、2、3 7分
的可能取值为0、1、2、3 7分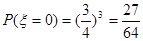 ;
; 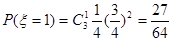
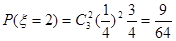 ;
;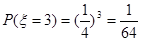
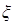 |  | 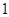 | 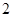 | 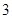 |
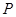 | 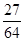 | 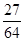 | 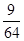 | 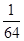 |
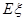
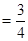 . 12分
. 12分

 活力课时同步练习册系列答案
活力课时同步练习册系列答案科目:高中数学 来源:不详 题型:解答题
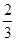 和
和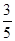 ,现安排甲组研发新产品
,现安排甲组研发新产品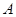 ,乙组研发新产品
,乙组研发新产品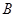 .设甲,乙两组的研发是相互独立的.
.设甲,乙两组的研发是相互独立的.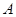 研发成功,预计企业可获得
研发成功,预计企业可获得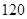 万元,若新产品
万元,若新产品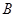 研发成功,预计企业可获得利润
研发成功,预计企业可获得利润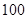 万元,求该企业可获得利润的分布列和数学期望.
万元,求该企业可获得利润的分布列和数学期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| 零件数x(个) | 10 | 20 | 30 |
| 加工时间y(分钟) | 21 | 30 | 39 |
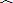 |
| y |
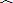 |
| b |
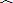 |
| a |
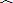 |
| b |
| A.84分钟 | B.94分钟 | C.102分钟 | D.112分钟 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
| 晚上 | 白天 | 总计 | |
| 男婴 | 45 | A | B |
| 女婴 | E | 35 | C |
| 总计 | 98 | D | 180 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
A.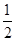 | B.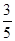 | C.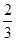 | D.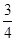 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com