
| 零件数x(个) | 10 | 20 | 30 |
| 加工时间y(分钟) | 21 | 30 | 39 |
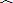 |
| y |
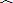 |
| b |
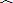 |
| a |
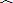 |
| b |
| A.84分钟 | B.94分钟 | C.102分钟 | D.112分钟 |
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源:不详 题型:解答题
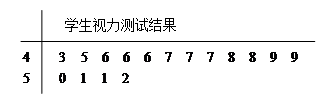
 表示抽到“好视力”学生的人数,求
表示抽到“好视力”学生的人数,求 的分布列及数学期望.
的分布列及数学期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 房屋面积(m2) | 115 | 110 | 80 | 135 | 105 |
| 销售价格(万元) | 24.8 | 21.6 | 18.4 | 29.2 | 22 |
| ? |
| b |
| |||||||
|
| ? |
| a |
| . |
| y |
| ? |
| b |
| . |
| x |
| 5 |
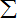 |
| i=1 |
| 5 |
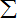 |
| i=1 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 广告支出x(单位:万元) | 1 | 2 | 3 | 4 |
| 销售收入y(单位:万元) | 12 | 28 | 42 | 56 |
| ? |
| y |
|
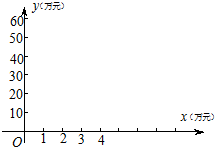
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 |
| y |
 |
| b |
 |
| a |
 |
| b |
 |
| a |
 |
| b |
 |
| a |
 |
| b |
 |
| a |
 |
| b |
x1y1+x2y2+x3y3-3
| ||||
x12+x22-3
|
 |
| a |
| . |
| y |
 |
| b |
| . |
| x |
| . |
| y |
| x | 2 | 3 | 4 | 5 | 6 | 7 |
| y | 4 | 6 | 5 | 6.2 | 8 | 7.1 |
 |
| b |
 |
| a |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| 成本费用x(万元) | 2 | 3 | 4 | 5 |
| 销售额y(万元) | 26 | 39 | 49 | 54 |
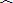 |
| y |
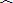 |
| b |
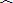 |
| a |
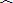 |
| b |
| A.72.0万元 | B.67.7万元 | C.65.5万元 | D.63.6万元 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
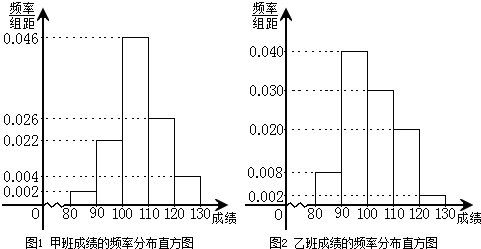
| 成绩小于100分 | 成绩不小于100分 | 合计 | |
| 甲班 | a=______ | b=______ | 50 |
| 乙班 | c=24 | d=26 | 50 |
| 合计 | e=______ | f=______ | 100 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.204 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com