
 |
| y |
 |
| b |
 |
| a |
 |
| b |
 |
| a |
 |
| b |
 |
| a |
 |
| b |
 |
| a |
 |
| b |
x1y1+x2y2+x3y3-3
| ||||
x12+x22-3
|
 |
| a |
| . |
| y |
 |
| b |
| . |
| x |
| . |
| y |
| x | 2 | 3 | 4 | 5 | 6 | 7 |
| y | 4 | 6 | 5 | 6.2 | 8 | 7.1 |
 |
| b |
 |
| a |
| . |
| x |
| . |
| y |
 |
| b |
x1y1+x2y2+x3y3-3
| ||||
x12+x22-3
|
 |
| b |
| 2×4+3×6+4×5-3×3×5 |
| 22+32+42-3×32 |
| 1 |
| 2 |
 |
| y |
 |
| b |
 |
| a |
| 1 |
| 2 |
 |
| a |
 |
| a |
| 7 |
| 2 |
 |
| y |
| 1 |
| 2 |
| 7 |
| 2 |
 |
| b |
 |
| a |
 |
| b |
 |
| a |
| 2 |
| 3 |


 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:高中数学 来源:不详 题型:单选题
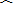 |
| y |
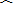 |
| b |
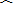 |
| a |
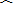 |
| y |
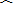 |
| b |
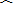 |
| a |
| x1+x2+…+x10 |
| 10 |
| y1+y2+…y10 |
| 10 |
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 50 | 60 | 70 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.相关指数R2为0.86的模型1 |
| B.相关指数R2为0.96的模型2 |
| C.相关指数R2为0.73的模型3 |
| D.相关指数R2为0.66的模型4 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| 零件数x(个) | 10 | 20 | 30 |
| 加工时间y(分钟) | 21 | 30 | 39 |
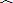 |
| y |
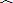 |
| b |
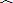 |
| a |
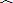 |
| b |
| A.84分钟 | B.94分钟 | C.102分钟 | D.112分钟 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
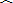 |
| y |
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | t | 4 | 4.5 |
| A.3 | B.3.15 | C.3.5 | D.4.5 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| 年龄x | 6 | 7 | 8 | 9 |
| 身高y | 118 | 126 | 136 | 144 |
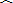 |
| y |
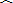 |
| a |
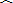 |
| y |
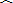 |
| b |
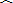 |
| a |
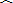 |
| a |
| . |
| y |
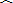 |
| b |
| . |
| x |
| A.154 | B.153 | C.152 | D.151 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 看法 性别 | 赞同 | 反对 | 合计 |
| 男 | 198 | 217 | 415 |
| 女 | 476 | 107 | 585 |
| 合计 | 674 | 326 | 1000 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com