已知数列{an}中,a1=1,a2=r(r>0)且an+2=qan(q>0,q≠1),又设bn=a2n-1-a2n(n=1,2,3,…)
(Ⅰ)求数列{bn}的通项bn及前n项和Sn;
(Ⅱ)假设对任意n>1都有Sn>bn,求r的取值范围.
解:(1)由题意可得 bn=a
2n-1-a
2n =qa
2n-3-qa
2n-2 =q(a
2n-3-a
2n-2)=qb
n-1,
故数列{b
n}是以q为公比的等比数列,b
1=a
1-a
2=1-r,
∴
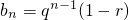
,
由等比数列前n项和公式求得
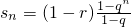
.
(2)∵对任意n>1都有S
n>b
n,
∴s
2>b
2,即
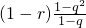
>q
n-1(1-r),即 (1-r)(1+q)>q(1-r).
再由 1+q>q>0,可得 1-r>0,∴r<1.
又r>0,∴1>r>0,即 r∈(0,1),
故r的取值范围为 (0,1).
分析:(1)由题意可得 bn=a
2n-1-a
2n =qa
2n-3-qa
2n-2 =q(a
2n-3-a
2n-2)=qb
n-1,故数列{b
n}是以q为公比的等比数列,b
1=a
1-a
2=1-r,由此求得数列{b
n}的通项b
n及前n项和S
n .
(2)由于 对任意n>1都有S
n>b
n,故 s
2>b
2,化简可得 (1-r)(1+q)>q(1-r).再由 1+q>q>0,可得 1-r>0,再结合条件求得r的取值范围.
点评:本题主要考查根据递推关系求数列的通项公式,等比关系的确定,等比数列的前n项和公式的应用,属于中档题.

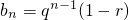 ,
,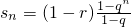 .
.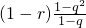 >qn-1(1-r),即 (1-r)(1+q)>q(1-r).
>qn-1(1-r),即 (1-r)(1+q)>q(1-r).
