
���� ��1������֪����������¼����ʳ˷���ʽ�ͻ����¼����ʼӷ���ʽ���������ӦƸ�ɹ�����������������ӦƸ�ɹ��������ĸ��ʣ�
��2������֪��X��ȡ0��1��2��3��4���ֱ������Ӧ�ĸ��ʣ��ɴ������X�ķֲ��к�������
��� �⣺��1������֪�ò���ӦƸ�ɹ�����������������ӦƸ�ɹ��������ĸ��ʣ�
P=$\frac{1}{3}��\frac{1}{2}��2����\frac{1}{2}��^{2}$$+\frac{1}{3}��\frac{1}{3}��\frac{3}{4}$=$\frac{7}{36}$����3�֣�
��2������֪��X��ȡ0��1��2��3��4��
P��X=0��=$\frac{2}{3}��\frac{2}{3}��\frac{1}{2}��\frac{1}{2}$=$\frac{4}{36}$��
P��X=1��=${C}_{2}^{1}��\frac{1}{3}��\frac{2}{3}��\frac{1}{2}��\frac{1}{2}$+${C}_{2}^{1}��\frac{2}{3}��\frac{2}{3}��\frac{1}{2}��\frac{1}{2}$=$\frac{12}{36}$��
P��X=2��=$\frac{1}{3}��\frac{1}{3}��\frac{1}{2}��\frac{1}{2}$+${C}_{2}^{1}{C}_{2}^{1}��\frac{1}{3}��\frac{2}{3}��\frac{1}{2}��\frac{1}{2}$+$\frac{2}{3}��\frac{2}{3}��\frac{1}{2}��\frac{1}{2}$=$\frac{13}{36}$��
P��X=3��=${C}_{2}^{1}��\frac{1}{3}��\frac{2}{3}��\frac{1}{2}��\frac{1}{2}$+${C}_{2}^{1}��\frac{1}{3}��\frac{1}{3}��\frac{1}{2}��\frac{1}{2}$=$\frac{6}{36}$��
P��X=4��=$\frac{1}{3}��\frac{1}{3}��\frac{1}{2}��\frac{1}{2}$=$\frac{1}{36}$��
��X�ķֲ���Ϊ
| X | 0 | 1 | 2 | 3 | 4 |
| P | $\frac{4}{36}$ | $\frac{12}{36}$ | $\frac{13}{36}$ | $\frac{6}{36}$ | $\frac{1}{36}$ |
���� ���⿼����ʵ���������ɢ����������ķֲ��к���ѧ��������ְ�����е��⣬����ʱҪע��������¼����ʳ˷���ʽ�ͻ����¼����ʼӷ���ʽ��������ã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
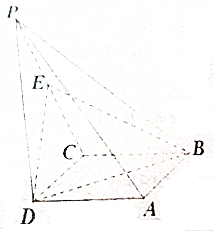 ��ͼ��������P-ABCD�У�����ABCD��ƽ���ı��Σ���DBC=45�㣬$\frac{BD}{BC}$=$\sqrt{2}$������PD�͵���ABCD��PD=CD��E��PC���е㣮
��ͼ��������P-ABCD�У�����ABCD��ƽ���ı��Σ���DBC=45�㣬$\frac{BD}{BC}$=$\sqrt{2}$������PD�͵���ABCD��PD=CD��E��PC���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3 | B�� | $\frac{8}{3}$ | C�� | 4 | D�� | 5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
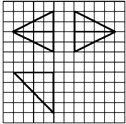 ��ͼ������ֽ��С�����εı߳�Ϊ1����ʵ��������ij�����������ͼ����ö�����ĸ������У������ij���Ϊ��������
��ͼ������ֽ��С�����εı߳�Ϊ1����ʵ��������ij�����������ͼ����ö�����ĸ������У������ij���Ϊ��������| A�� | 2$\sqrt{5}$ | B�� | 2$\sqrt{6}$ | C�� | 4$\sqrt{2}$ | D�� | 4$\sqrt{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com