解答:
解:(1)
f′(x)==,令f′(x)=0,得x=1,
当a>0时,如果x∈(1,+∞),那么f′(x)<0,因此(1,+∞)为函数的单调减区间;如果x∈(-∞,1),那么f′(x)>0,因此(-∞,1)为函数的单调增区间.
当a<0时,如果x∈(1,+∞),那么f′(x)>0,因此(1,+∞)为函数的单调增区间;如果x∈(-∞,1),那么f′(x)<0,因此(-∞,1)为函数的单调减区间.
(2)当a=1时,f(x)=
,由(1)知,(1,+∞)为函数的单调减区间;(-∞,1)为函数的单调增区间.
又f(0)=0,f(1)=
,函数f(x)的图象:
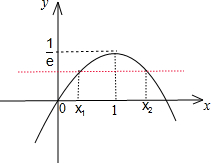
∵x
1<x
2,且f(x
1)=f(x
2),∴从图象上看,x
1<1,x
2>1,
f(x
1)>f(2-x
2)?f(x
2)>f(2-x
2),∴要证f(x
1)>f(2-x
2)只要证明x
2>1时f(x
2)-f(2-x
2)>0即可:
构造函数g(x)=f(x)-f(2-x),即g(x)=
-
,下面证明:对于?x>1,g(x)>0恒成立,
则g′(x)=
-=
,
如果x∈(1,+∞),那么x-1>0,e
2(x-1)>1,则(1-x)(1-e
2(x-1))>0,因此g′(x)>0,因此g(x)在(1,+∞)上为单调增函数;
∴g(x)在(1,+∞)上单调递增,
在x∈[1,+∞)时:当x=1时,函数g(x)取最小值,即
g最小值=g(1)=-=0,∴对于?x∈(1,+∞),g(x)>0恒成立,
∴x
2>1时f(x
2)-f(2-x
2)>0,∴f(x
2)>f(2-x
2),
又∵f(x
1)=f(x
2),
∴f(x
1)>f(2-x
2).



