
已知点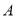 、
、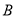 、
、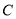 、
、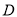 的坐标分别为
的坐标分别为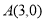 、
、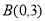 、
、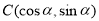 、
、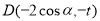 ,
,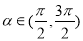
(1)若|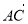 |=|
|=|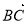 |,求角
|,求角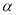 的值;
的值;
(2)若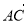 ·
·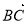 =
=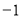 ,求
,求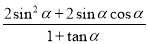 的值.
的值.
(3)若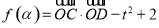 在定义域
在定义域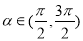 有最小值
有最小值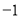 ,求
,求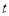 的值.
的值.
(1) ;(2)
;(2) ;(3)
;(3)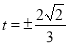 .
.
【解析】
试题分析:(1)根据已知A,B,C,D四点的坐标可以把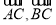 的坐标分别求得,即有
的坐标分别求得,即有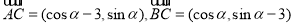 ,又根据
,又根据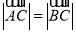 可以建立关于
可以建立关于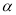 的方程,求得
的方程,求得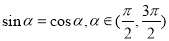 ,从而
,从而 ;(2)由平面向量数量积的坐标表示,
;(2)由平面向量数量积的坐标表示,
可得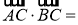
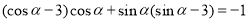 ,化简可得
,化简可得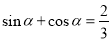 ,再将要求值的表达式化简为
,再将要求值的表达式化简为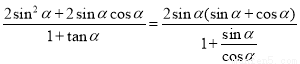
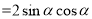 ,
,
由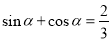 ,可求得
,可求得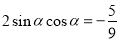 ,从而需求值的表达式的值为
,从而需求值的表达式的值为 ;
;
(3)根据已知条件中点的坐标,可求得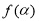
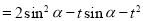 ,若令
,若令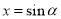 ,则问题等价于当
,则问题等价于当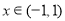 时,求使
时,求使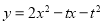 最小值为-1的
最小值为-1的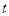 的值,显然
的值,显然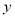 是关于
是关于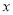 的开口向上的二次函数,若其在
的开口向上的二次函数,若其在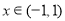 时,存在最小值,则必有对称轴
时,存在最小值,则必有对称轴 ,且当
,且当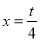 时,
时, 取到最小值-1,从而建立了关于
取到最小值-1,从而建立了关于 的方程,可解得
的方程,可解得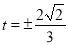 .
.
(1)又条件可得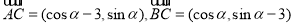 ,又∵
,又∵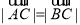 ,
,
∴  ,
,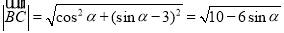
由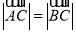 得
得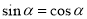 ,又
,又
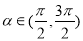 ,∴
,∴ 5分;
5分;
(2)由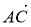 ·
· =
=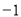 得
得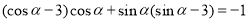 ,
,
∴ 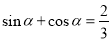 ① 6分
① 6分
又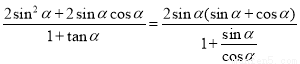
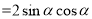 7分
7分
由①式两边平方得 ∴
∴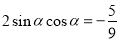 8分
8分
∴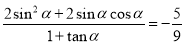 . 9分;
. 9分;
依题意记
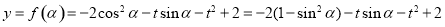
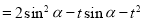 10分
10分
令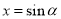 ,
,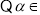 (
(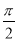 ,
,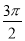 ),
),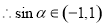 ,
,
则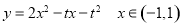 11分
11分
关于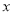 的二次函数开口向上,对称轴为
的二次函数开口向上,对称轴为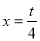 ,
,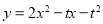 在
在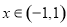 上存在最小值,则对称轴
上存在最小值,则对称轴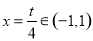
 12分
12分
且当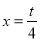 时,
时,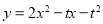 取最小值为
取最小值为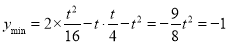
 14分
14分
考点:1.平面向量的数量积与模的坐标表示;2.三角函数与二次函数综合.


科目:高中数学 来源:2016届河北省高一下学期期中考试理科数学试卷(解析版) 题型:选择题
设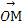 =(1,1),
=(1,1),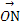 =(3,1),O为坐标原点,动点P(x,y)满足0≤
=(3,1),O为坐标原点,动点P(x,y)满足0≤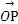 ·
·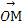 ≤1,0≤
≤1,0≤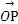 ·
·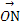 ≤1,则
≤1,则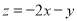 的最大值是 ( )
的最大值是 ( )
A.0 B.1 C.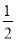 D.
D.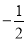
查看答案和解析>>
科目:高中数学 来源:2016届江西省高一下学期第二次月考数学试卷(解析版) 题型:选择题
在从2011年到2014年期间,甲每年1月1日都到银行存入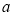 元的一年定期储蓄。若年利率为
元的一年定期储蓄。若年利率为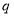 保持不变,且每年到期的存款本息均自动转为新的一年定期储蓄,到2014年1月1日,甲去银行不再存款,而是将所有存款的本息全部取回,则取回的金额是( )元.
保持不变,且每年到期的存款本息均自动转为新的一年定期储蓄,到2014年1月1日,甲去银行不再存款,而是将所有存款的本息全部取回,则取回的金额是( )元.
A.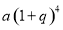 B.
B.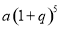
C.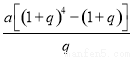 D.
D.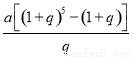
查看答案和解析>>
科目:高中数学 来源:2016届江西省高一下学期期中考试文科数学试卷(解析版) 题型:解答题
(1)化简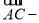
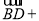
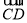
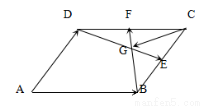
(2)如图,平行四边形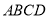 中,
中, 分别是
分别是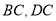 的中点,
的中点,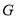 为
为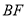 与
与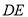 的交点,若
的交点,若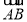 =
=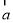 ,
,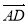 =
=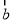 ,试以
,试以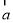 ,
,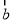 为基底表示
为基底表示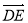 、
、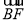 、
、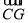 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com