
 )相乘和1004个
)相乘和1004个 相乘,根据数列的规律,利用乘法的法则,即可得到该数列的前2009项的积.
相乘,根据数列的规律,利用乘法的法则,即可得到该数列的前2009项的积.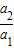 =
=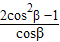 =q=-1,
=q=-1, 或cosβ=-1,
或cosβ=-1, ,-
,- ,
, ,…,-
,…,- ,
,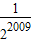 .
.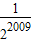


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2014届河北省高一下学期期中数学试卷(解析版) 题型:选择题
若数列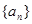 ,
,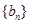 均为公比不是1的等比数列,设
均为公比不是1的等比数列,设 (
( ),那么数列
),那么数列
A.一定是等比数列
B.一定不是等比数列
C.有可能是等比数列,也有可能不是等比数列
D.一定不是等差数列
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com