练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    以初速度40,垂直向上抛一物体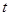，时刻的速度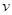（的单位是）为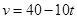，则该物体达到最大高度为            .米
    80

    先求物体达到最大高度即其速度为0时，物体运动时间，再将物体最大高度问题转化为速度函数在时间上的定积分问题，利用微积分基本定理计算定积分的值即得最大高度
    解：令v=0，得t=4

    故答案为 80
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：不详 题型：单选题

    已知，那么的值是            （   ）
    A．3B．2C．1D．0

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    函数在区间上是减函数，则实数的取值范围(　)
    A．B．C．D．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

     设函数与的定义域是,函数是一个偶函数，是一个奇函数，且，则等于(    )
    A．B．C．D．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    某种出口产品的关税税率t．市场价格x(单位：千元)与市场供应量p(单位：万件)之间近似满足关系式：，其中k．b均为常数．当关税税率为75%时，若市场价格为5千元，则市场供应量约为1万件；若市场价格为7千元，则市场供应量约为2万件．
    (1)试确定k．b的值；
    (2)市场需求量q(单位：万件)与市场价格x近似满足关系式：．P = q时，市场价格称为市场平衡价格．当市场平衡价格不超过4千元时，试确定关税税率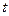的最大值．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    已知函数满足:对任意实数,当时,总有,那么实数的取值范围是 （     ）
    A．B．C．D．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

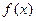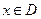    （本题满分10分）已知函数,()，若同时满足以下条件：
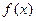    ①在D上单调递减或单调递增
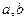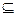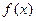    ② 存在区间[]D,使在[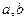]上的值域是[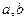]，那么称()为闭函数。
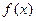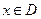    （1）求闭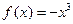函数符合条件②的区间[]；
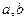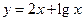    （2）判断函数是不是闭函数？若是请找出区间[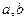]；若不是请说明理由；
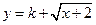    （3）若是闭函数，求实数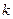的取值范围.

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    函数 的定义域为（   ）
    A．B．C．D．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    =      

    查看答案和解析>>

    同步练习册答案