
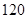 分为优秀,
分为优秀,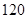 分以下为非优秀,统计成绩后,得到如下的
分以下为非优秀,统计成绩后,得到如下的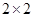 列联表,且已知在甲、乙两个文科班全部
列联表,且已知在甲、乙两个文科班全部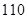 人中随机抽取人为优秀的概率为
人中随机抽取人为优秀的概率为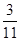 .
.| | 优秀 | 非优秀 | 合计 |
| 甲班 |  | | |
| 乙班 | | 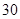 | |
| 合计 | | | 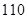 |
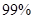 的把握认为成绩与班级有关系?
的把握认为成绩与班级有关系? 表示抽得甲班的学生人数,求
表示抽得甲班的学生人数,求 的分布列.
的分布列.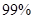 的可靠性要求,能认为“成绩与班级有关系”;
的可靠性要求,能认为“成绩与班级有关系”; 或
或 号的概率为
号的概率为 .
. 的值,然后利用临界值表确定犯错误的概率,进而确定是否有
的值,然后利用临界值表确定犯错误的概率,进而确定是否有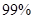 的把握认为成绩与班级有关系;(3)先确定随机变量
的把握认为成绩与班级有关系;(3)先确定随机变量 的可能取值,然后根据超几何分布的方法求出随机变量
的可能取值,然后根据超几何分布的方法求出随机变量 在相应的取值下的概率,并列出相应的分布列.
在相应的取值下的概率,并列出相应的分布列.| | 优秀 | 非优秀 | 合计 |
| 甲班 |  | 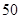 | 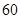 |
| 乙班 | 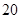 | 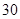 | 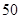 |
| 合计 | 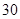 | 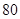 | 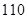 |
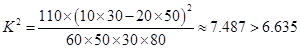 ,
,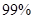 的可靠性要求,能认为“成绩与班级有关系”;
的可靠性要求,能认为“成绩与班级有关系”; 、
、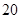 ,
, 的可能取值为
的可能取值为 、
、 、
、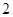 ,
,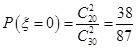 ,
,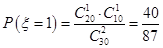 ,
, ,
, 的分布列为:
的分布列为: |  |  | 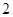 |
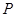 | 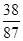 |  |  |


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:不详 题型:解答题
 ,乙能答对其中的5道题.规定每次考试都从备选的10道题中随机抽出3道题进行测试,答对一题加10分,答错一题(不答视为答错)减5分,得分最低为0分,至少得15分才能入选.
,乙能答对其中的5道题.规定每次考试都从备选的10道题中随机抽出3道题进行测试,答对一题加10分,答错一题(不答视为答错)减5分,得分最低为0分,至少得15分才能入选.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
A.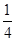 | B. | C.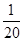 | D.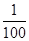 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
A.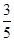 ; ; | B.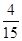 ; ; | C.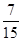 ; ; | D. . . |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.1/3 | B.1/4 | C.1/5 | D.1/6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com