
【题目】某种产品的质量以其质量指标值衡量,并依据质量指标值划分等级如下表:
质量指标值 |
|
|
|
等级 | 三等品 | 二等品 | 一等品 |
从某企业生产的这种产品中抽取200件,检测后得到如下的频率分布直方图:
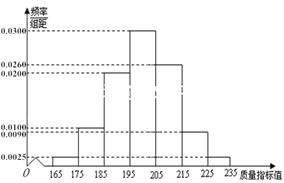
(Ⅰ)根据以上抽样调查数据,能否认为该企业生产的这种产品符合“一、二等品至少要占全部产品92%”的规定?
(Ⅱ)在样本中,按产品等级用分层抽样的方法抽取8件,再从这8件产品中随机抽取4件,求抽取的4件产品中,一、二、三等品都有的概率;
(Ⅲ)该企业为提高产品质量,开展了“质量提升月”活动,活动后再抽样检测,产品质量指标值![]() 近似满足
近似满足![]() ,则“质量提升月”活动后的质量指标值的均值比活动前大约提升了多少?
,则“质量提升月”活动后的质量指标值的均值比活动前大约提升了多少?
【答案】(Ⅰ)见解析; (Ⅱ)![]() ;(Ⅲ)大约提升了17.6
;(Ⅲ)大约提升了17.6
【解析】试题分析:(1)根据频率分布直方图,一、二等品所占比例的估计值为
![]() ,可做出判断.
,可做出判断.
(2)由频率分布直方图的频率分布可知8件产品中,一等品3件,二等品4件,三等品1件,分类讨论各种情况可得![]() .
.
(3)算出“质量提升月”活动前,后产品质量指标值为![]() ,可得质量指标值的均值比活动前大约提升了17.6
,可得质量指标值的均值比活动前大约提升了17.6
试题解析:(1)根据抽样调查数据,一、二等品所占比例的估计值为![]() ,由于该估计值小于0.92,故不能认为该企业生产的这种产品符合“一、二等品至少要占全部产品92%”的规定.
,由于该估计值小于0.92,故不能认为该企业生产的这种产品符合“一、二等品至少要占全部产品92%”的规定.
(2)由频率分布直方图知,一、二、三等品的频率分别为0.375、0.5、0.125,故在样本中用分层抽样方法抽取的8件产品中,一等品3件,二等品4件,三等品1件,再从这8件产品中随机抽取4件,一、二、三等品都有的情况有2种:①一等品2件,二等品1件,三等品1件;②一等品1件,二等品2件,三等品1件,故所求的概率![]() .
.
(3)“质量提升月”活动前,该企业这种产品的质量指标值的均值约为
![]()
![]()
“质量提升月”活动后,产品质量指标值![]() 近似满足
近似满足![]() ,则
,则![]() .
.
所以,“质量提升月”活动后的质量指标值的均值比活动前大约提升了17.6


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】交通指数是交通拥堵指数的简称,是综合反映道路网畅通或拥堵的概念.记交通指数为![]() ,其范围为
,其范围为![]() ,分别有5个级别:
,分别有5个级别:![]() 畅通;
畅通;![]() 基本畅通;
基本畅通;![]() 轻度拥堵;
轻度拥堵;![]() 中度拥堵;
中度拥堵;![]() 严重拥堵.早高峰时段(
严重拥堵.早高峰时段(![]() ),从贵阳市交通指挥中心随机选取了二环以内50个交通路段,依据交通指数数据绘制的直方图如图所示:
),从贵阳市交通指挥中心随机选取了二环以内50个交通路段,依据交通指数数据绘制的直方图如图所示:

(1)据此直方图估算交通指数![]() 时的中位数和平均数;
时的中位数和平均数;
(2)据此直方图求出早高峰二环以内的3个路段至少有两个严重拥堵的概率是多少?
(3)某人上班路上所用时间若畅通时为20分钟,基本畅通为30分钟,轻度拥堵为35分钟,中度拥堵为45分钟,严重拥堵为60分钟,求此人所用时间的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的焦点在
的焦点在![]() 轴上,椭圆
轴上,椭圆![]() 的左顶点为
的左顶点为![]() ,斜率为
,斜率为![]() 的直线交椭圆
的直线交椭圆![]() 于
于![]() ,
, ![]() 两点,点
两点,点![]() 在椭圆
在椭圆![]() 上,
上, ![]() ,直线
,直线![]() 交
交![]() 轴于点
轴于点![]() .
.
(Ⅰ)当点![]() 为椭圆的上顶点,
为椭圆的上顶点, ![]() 的面积为
的面积为![]() 时,求椭圆的离心率;
时,求椭圆的离心率;
(Ⅱ)当![]() ,
, ![]() 时,求
时,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个袋中装有四个形状大小完全相同的球,球的编号分别为1,2,3,4.
(1)从袋中随机抽取两个球,求取出的球的编号之和不大于4的概率;
(2)先从袋中随机取一个球,该球的编号为m,将球放回袋中,然后再从袋中随机取一个球,该球的编号为n,求n<m+2的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=2x2﹣3x+1,g(x)=ksin(x﹣ ![]() )(k≠0).
)(k≠0).
(1)设f(x)的定义域为[0,3],值域为A; g(x)的定义域为[0,3],值域为B,且AB,求实数k的取值范围.
(2)若方程f(sinx)+sinx﹣a=0在[0,2π)上恰有两个解,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为大力提倡“厉行节约,反对浪费”,某市通过随机询问100名性别不同的居民是否能做到“光盘”行动,得到如下的列联表:( )
做不到“光盘” | 能做到“光盘” | |
男 | 45 | 10 |
女 | 30 | 15 |
附:
P(K2 | 0.10 | 0.05 | 0.025 |
k | 2.706 | 3.841 | 5.024 |
![]()
参照附表,得到的正确结论是
A.在犯错误的概率不超过l%的前提下,认为“该市居民能否做到‘光盘’与性别有关”
B.在犯错误的概率不超过l%的前提下,认为“该市居民能否做到‘光盘’与性别无关”
C.有90%以上的把握认为“该市居民能否做到‘光盘’与性别有关”
D.有90%以上的把握认为“该市居民能否做到‘光盘’与性别无关”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(sinx+cosx)2+2cos2x﹣2.
(1)求函数f(x)的最小正周期和单调增区间;
(2)当x∈[ ![]() ,
, ![]() ]时,求函数f(x)的最大值,最小值.
]时,求函数f(x)的最大值,最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校的特长班有50名学生,其中有体育生20名,艺术生30名,在学校组织的一次体检中,该班所有学生进行了心率测试,心率全部介于50次/分到75次/分之间,现将数据分成五组,第一组![]() ,第二组
,第二组![]() ,…,第五组
,…,第五组![]() ,按上述分组方法得到的频率分布直方图如图所示,已知图中从左到右的前三组的频率之比为
,按上述分组方法得到的频率分布直方图如图所示,已知图中从左到右的前三组的频率之比为![]() .
.
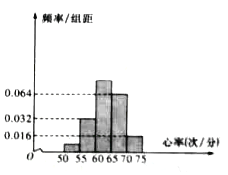
(Ⅰ)求![]() 的值,并求这50名同学心率的平均值;
的值,并求这50名同学心率的平均值;
(Ⅱ)因为学习专业的原因,体育生常年进行系统的身体锻炼,艺术生则很少进行系统的身体锻炼,若从第一组和第二组的学生中随机抽取一名,该学生是体育生的概率为0.8,请将下面的列联表补充完整,并判断是否有99.5%的把握认为心率小于60次/分与常年进行系统的身体锻炼有关?说明你的理由.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式: 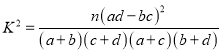 ,其中
,其中![]()
心率小于60次/分 | 心率不小于60次/分 | 合计 | |
体育生 | 20 | ||
艺术生 | 30 | ||
合计 | 50 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com