
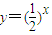 的图象与函数y=logax(a>0且a≠1)的图象交于点P(x,y),如果x≥2,那么a的取值范围是( )
的图象与函数y=logax(a>0且a≠1)的图象交于点P(x,y),如果x≥2,那么a的取值范围是( ) 的图象与函数y=logax(a>0且a≠1)的图象交于点P(x,y),如果x≥2,我们根据指数不等式的性质,求出y的范围,进而结合点P(x,y)也在函数y=logax的图象上,再由对数函数的性质,构造关于a的不等式,解不等式即可得到答案.
的图象与函数y=logax(a>0且a≠1)的图象交于点P(x,y),如果x≥2,我们根据指数不等式的性质,求出y的范围,进而结合点P(x,y)也在函数y=logax的图象上,再由对数函数的性质,构造关于a的不等式,解不等式即可得到答案. 的图象与函数y=logax(a>0且a≠1)的图象交于点P(x,y),
的图象与函数y=logax(a>0且a≠1)的图象交于点P(x,y),

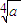 ≥x≥2
≥x≥2

科目:高中数学 来源: 题型:
(08年长沙一中一模理)已知函数![]() 的图象过点
的图象过点![]() ,且在
,且在![]() 内单调递减,在
内单调递减,在![]() 上单调递增.
上单调递增.
(1)证明![]() 并求
并求![]() 的解析式;
的解析式;
(2)若对于任意的![]() ,不等式
,不等式![]() 恒成立,试问这样的
恒成立,试问这样的![]() 是否存在.若存在,请求出
是否存在.若存在,请求出![]() 的范围,若不存在,说明理由;
的范围,若不存在,说明理由;
(3)已知数列![]() 中,
中,![]() 求证:
求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年惠州一中五模理) 已知函数![]() 的图象为曲线E.
的图象为曲线E.
(Ⅰ) 若曲线E上存在点P,使曲线E在P点处的切线与x轴平行,求a,b的关系;
(Ⅱ) 说明函数![]() 可以在
可以在![]() 和
和![]() 时取得极值,并求此时a,b的值;
时取得极值,并求此时a,b的值;
(Ⅲ) 在满足(2)的条件下,![]() 在
在![]() 恒成立,求c的取值范围.
恒成立,求c的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com