解(1)f(x)=lg
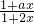
(-b<x<b)是奇函数等价于:
对任意x∈(-b,b)都有
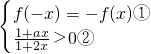
①式即为
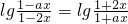
,由此可得
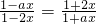
,
也即a
2x
2=4x
2,此式对任意x∈(-b,b)都成立相当于a
2=4,
因为a≠2,所以a=-2,
代入②式,得
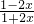
>0,即-

<x<

,
此式对任意x∈(-b,b)都成立相当于
-

≤-b<b≤

,
所以b的取值范围是(0,

].
(2)设任意的x
1,x
2∈(-b,b),且x
1<x
2,
由b∈(0,

],得-

≤-b<x
1<x
2<b≤

,
所以0<1-2x
2<1-2x
1,0<1+2x
1<1+2x
2,
从而f(x
2)-f(x
1)=
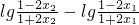
=
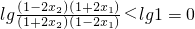
因此f(x)在(-b,b)内是减函数.
分析:(1)由函数f(x)在区间(-b,b)是奇函数,知f(-x)=-f(x),x∈(-b,b)上恒成立,用待定系数法求得a;同时函数要有意义,即

,x∈(-b,b)上恒成立,可解得结果.
(2)选用定义法求解,先任意取两个变量且界定大小,再作差变形看符号.
点评:本题主要考查函数的奇偶性,要注意定义域优先考虑原则,还考查了用定义法证明函数的单调性,要注意作差时的变形要到位,要用上两个变量的大小关系.

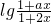 是奇函数.
是奇函数.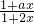 (-b<x<b)是奇函数等价于:
(-b<x<b)是奇函数等价于: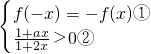
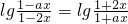 ,由此可得
,由此可得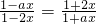 ,
,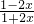 >0,即-
>0,即- <x<
<x< ,
, ≤-b<b≤
≤-b<b≤ ,
, ].
]. ],得-
],得- ≤-b<x1<x2<b≤
≤-b<x1<x2<b≤ ,
,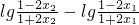
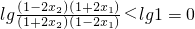
 ,x∈(-b,b)上恒成立,可解得结果.
,x∈(-b,b)上恒成立,可解得结果.
