练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】选修4-4：坐标系与参数方程

    在直角坐标系中，曲线的参数方程为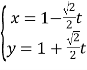（为参数），以坐标原点为极点，以轴正半轴为极轴建立极坐标系，曲线的极坐标方程为.

    （1）求曲线的普通方程与曲线的直角坐标方程；

    （2）若与交于两点，点的极坐标为，求的值.

    【答案】（1）曲线普通方程为曲线的直角坐标方程为（2）

    【解析】

    （1）将曲线的参数方程中的t消掉得到曲线的普通方程，利用ρcosθ＝x，ρsinθ＝y，能求出C2的直角坐标方程．

    （2）将代入，得，利用直线参数的几何意义结合韦达定理，能求出．

    （1）曲线的参数方程为（为参数），两式相加消去t可得普通方程为；又由ρcosθ＝x，ρsinθ＝y，

    曲线的极坐标方程为转化为直角坐标方程为

    （2）把曲线的参数方程为（为参数），代入得，

    设，是对应的参数，则，

    所以

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】在正方体ABCD﹣A1B1C1D1中，当点E在B1D1（与B1，D1不重合）上运动时，总有：

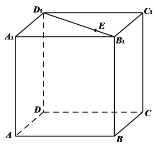
    ①AE∥BC1； ②平面AA1E⊥平面BB1D1D；

    ③AE∥平面BC1D； ④A1C⊥AE．

    以上四个推断中正确的是（ ）

    A.①②B.①④C.②④D.③④

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图,在多面体中,平面,四边形为正方形,四边形为梯形,且,,,.

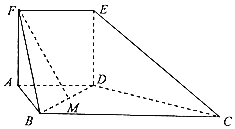
    (1)求直线与平面所成角的正弦值；

    (2)线段上是否存在点,使得直线平面？若存在,求的值：若不存在,请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知服从正态分布的随机变量在区间，，内取值的概率分别为0.6826，0.9544，0.9974.若某种袋装大米的质量（单位：）服从正态分布，任意选一袋这种大米，质量在的概率为_．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知p：x∈R，x2+2x≥a，q：x2﹣4x+3≤0，r：（x﹣m）[x﹣（m+1）]≤0．

    （1）若命题p的否定是假命题，求实数a的取值范围；

    （2）若q是r的必要条件，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设．

    讨论的单调区间；

    当时，在上的最小值为，求在上的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某仪器经过检验合格才能出厂，初检合格率为：若初检不合格，则需要进行调试，经调试后再次对其进行检验；若仍不合格，作为废品处理，再检合格率为.每台仪器各项费用如表：

    项目

    生产成本

    检验费/次

    调试费

    出厂价

    金额（元）

    1000

    100

    200

    3000

    （Ⅰ）求每台仪器能出厂的概率；

    （Ⅱ）求生产一台仪器所获得的利润为1600元的概率（注：利润出厂价生产成本检验费调试费）；

    （Ⅲ）假设每台仪器是否合格相互独立，记为生产两台仪器所获得的利润，求的分布列和数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆C： （a>b>0），四点P1（1,1），P2（0,1），P3（–1， ），P4（1， ）中恰有三点在椭圆C上.

    （1）求C的方程；

    （2）设直线l不经过P2点且与C相交于A，B两点.若直线P2A与直线P2B的斜率的和为–1，证明：l过定点.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）＝ex（x﹣a）2+4．

    （1）若f（x）在（﹣∞，+∞）上单调递增，求a的取值范围；

    （2）若x≥0，不等式f（x）≥0恒成立，求a的取值范围．

    查看答案和解析>>

    同步练习册答案