
【题目】已知![]()
(I)判断f(x)的奇偶性并证明
(Ⅱ)若a>1,判断f(x)的单调性并用单调性定义证明;
(Ⅲ)若![]() ,求实数x的取值范围
,求实数x的取值范围
【答案】(I)见解析;(II) 见解析;(III) ![]()
【解析】试题分析:(1)求解![]() 即可.
即可.
(2)运用单调性证明则f(x1)-f(x2)=loga![]() -loga
-loga![]() =loga
=loga![]() .判断符号即可.
.判断符号即可.
(3)根据单调性转化-1<x-3≤![]() 求解.
求解.
试题解析:(I)由![]() 得
得![]() ,∴函数f(x)的定义域为(-1,1) 关于原点对称.
,∴函数f(x)的定义域为(-1,1) 关于原点对称.
f(x)在(-1,1)上为奇函数,证明如下:
![]() ,
,
∴f(x)为(-1,1)上的奇函数.
(II) 若![]() ,f(x)在(-1,1)上单调递增,证明如下:
,f(x)在(-1,1)上单调递增,证明如下:
设-1<x1<x2<1, ![]()
则f(x1)-f(x2)=loga![]() -loga
-loga![]() =loga
=loga![]() .
.
又-1<x1<x2<1,
∴(1+x1)(1-x2)-(1-x1)(1+x2)=2(x1-x2)<0,
即0<(1+x1)(1-x2)<(1-x1)(1+x2),
∴0<![]() <1,∴loga
<1,∴loga![]() <0,
<0,
∴f(x1)<f(x2),∴f(x)在(-1,1)上单调递增.
(III)∵f(x)为(-1,1)上的奇函数,
∴f(x-3) ≤-f(-![]() )=f(
)=f(![]() ).
).
若![]() ,f(x)在(-1,1)上单调递增,
,f(x)在(-1,1)上单调递增,
∴-1<x-3≤![]() ,得2<x≤
,得2<x≤![]() .
.
若![]() ,f(x)在(-1,1)上单调递减,
,f(x)在(-1,1)上单调递减,
∴![]() ≤x-3<1,得
≤x-3<1,得![]() ≤x<4.
≤x<4.
综上可知,当![]() 时,实数x的取值范围为
时,实数x的取值范围为![]() ;
;
当![]() 时,实数x的取值范围为
时,实数x的取值范围为![]()
点晴:本题属于对函数单调性应用的考察,若函数![]() 在区间上单调递增,则
在区间上单调递增,则![]() 时,有
时,有![]() ,事实上,若
,事实上,若![]() ,则
,则![]() ,这与
,这与![]() 矛盾,类似地,若
矛盾,类似地,若![]() 在区间上单调递减,则当
在区间上单调递减,则当![]() 时有
时有![]() ;据此可以解不等式,由函数值的大小,根据单调性就可以得自变量的大小关系.本题中的易错点是容易忽视定义域(-1,1).
;据此可以解不等式,由函数值的大小,根据单调性就可以得自变量的大小关系.本题中的易错点是容易忽视定义域(-1,1).


科目:高中数学 来源: 题型:
【题目】2018年1曰8日,中共中央、国务院隆重举行国家科学技术奖励大会,在科技界引发热烈反响,自主创新正成为引领经济社会发展的强劲动力.某科研单位在研发新产品的过程中发现了一种新材料,由大数据测得该产品的性能指标值![]() 与这种新材料的含量
与这种新材料的含量![]() (单位:克)的关系为:当
(单位:克)的关系为:当![]() 时,
时, ![]() 是
是![]() 的二次函数;当
的二次函数;当![]() 时,
时, ![]() .测得数据如表(部分)
.测得数据如表(部分)
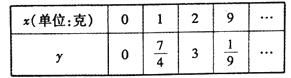
(1)求![]() 关于
关于![]() 的函数关系式
的函数关系式![]() ;
;
(2)其函数![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sinx,若存在x1 , x2 , ,xm满足0≤x1<x2<xm≤6π,且|f(x1)﹣f(x2)|+|f(x2)﹣f(x3)|+|f(xn﹣1)﹣f(xn)|=12,(m≥2,m∈N*),则m的最小值为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经过市场调查,某种商品在销售中有如下关系:第![]() 天的销售价格(单位:元/件)为
天的销售价格(单位:元/件)为![]() ,第
,第![]() 天的销售量(单位:件)为
天的销售量(单位:件)为![]() (
(![]() 为常数),且在第20天该商品的销售收入为1200元(
为常数),且在第20天该商品的销售收入为1200元(![]() ).
).
(Ⅰ)求![]() 的值,并求第15天该商品的销售收入;
的值,并求第15天该商品的销售收入;
(Ⅱ)求在这30天中,该商品日销售收入![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数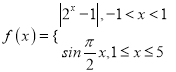 ,有如下结论
,有如下结论
①函数f(x)的值域是[-1,1];
②函数f(x)的减区间为[1,3];
③若存在实数x1、x2、x3、x4,满足x1<x2<x3<x4,且f(x1)=f(x2)=f(x3)=f(x4),则x1+x2<0;
④在③的条件下x3+x4=6;
⑤若方程f(x)=a有3个解,则![]() <a≤1
<a≤1
其中正确的是
A. ①②③ B. ③④⑤ C. ②③⑤ D. ①③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】集合![]() 由满足以下性质的函数
由满足以下性质的函数![]() 组成:①
组成:①![]() 在
在![]() 上是增函数;②对于任意的
上是增函数;②对于任意的![]() ,
, ![]() .已知函数
.已知函数![]() ,
, ![]() .
.
(1)试判断![]() ,
, ![]() 是否属于集合
是否属于集合![]() ,并说明理由;
,并说明理由;
(2)将(1)中你认为属于集合![]() 的函数记为
的函数记为![]() .
.
(ⅰ)试用列举法表示集合![]() ;
;
(ⅱ)若函数![]() 在区间
在区间![]() 上的值域为
上的值域为![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() 的离心率为
的离心率为 ![]() ,它的一个焦点到短轴顶点的距离为2,动直线l:y=kx+m交椭圆E于A、B两点,设直线OA、OB的斜率都存在,且
,它的一个焦点到短轴顶点的距离为2,动直线l:y=kx+m交椭圆E于A、B两点,设直线OA、OB的斜率都存在,且 ![]() .
.
(1)求椭圆E的方程;
(2)求证:2m2=4k2+3;
(3)求|AB|的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某县政府为了引导居民合理用水,决定全面实施阶梯水价,阶梯水价原则上以住宅(一套住宅为一户)的月用水量为基准定价:若用水量不超过12吨时,按4元/吨计算水费;若用水量超过12吨且不超过14吨时,超过12吨部分按6.60元/吨计算水费;若用水量超过14吨时,超过14吨部分按7.80元/吨计算水费.为了了解全市居民月用水量的分布情况,通过抽样,获得了100户居民的月用水量(单位:吨),将数据按照![]() ,
,![]() ,…,
,…,![]() 分成8组,制成了如图1所示的频率分布直方图.
分成8组,制成了如图1所示的频率分布直方图.
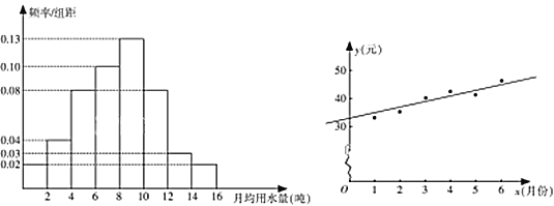
(图1) (图2)
(Ⅰ)通过频率分布直方图,估计该市居民每月的用水量的平均数和中位数(精确到0.01);
(Ⅱ)求用户用水费用![]() (元)关于月用水量
(元)关于月用水量![]() (吨)的函数关系式;
(吨)的函数关系式;
(Ⅲ)如图2是该县居民李某2017年1~6月份的月用水费![]() (元)与月份
(元)与月份![]() 的散点图,其拟合的线性回归方程是
的散点图,其拟合的线性回归方程是![]() .若李某2017年1~7月份水费总支出为294.6元,试估计李某7月份的用水吨数.
.若李某2017年1~7月份水费总支出为294.6元,试估计李某7月份的用水吨数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在等腰直角三角形![]() 中,
中,![]() ,
,![]() ,
,![]() 、
、![]() 分别是
分别是![]() ,
,![]() 上的点,
上的点,![]() ,
,![]() 为
为![]() 的中点,将
的中点,将![]() 沿
沿![]() 折起,得到如图2所示的四棱锥
折起,得到如图2所示的四棱锥![]() ,其中
,其中![]() .
.

(1)证明:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的平面角的余弦值;
的平面角的余弦值;
(3)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com