练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    己知等差数列{An}的公差d≠0，数列{Bn}是等比数列.又A1=B1=1,A2=B2,A4=B4。

    (1)   求数列{An}及数列{Bn}的通项公式；

    （2）设Cn=An·Bn,求数列{Cn}的前n项的和Sn（写成关于n的表达式）.

    答案：
    解析：

    		（1）设等比数列{Bn}的公比为q,则

     

    把第一个等式代入第二个，得d2+3d2=0.

    ∵d≠0，∴d=－3.并求得q=－2.

    ∴An=－3n+4,Bn=(－2)n－1(n∈N*)

    （2）由（1）知Cn=AnBn=(－3n+4)·(－2)n－1,

    Sn=C1+C2+C3+…+Cn=1+(－2)·(－2)+……+(－3n+4)(－2)n－1.

    而－2Sn=(－2)+(－2)(－2)2+…+(－3n+7)·(－2)n－1+(－3n+4)(－2)n,

    3Sn=1+(－3)[(－2)+(－2)2+…+(－2)n－1]－(－3n+4)(－2)n

    =1+(－3)－(－3n+4)(－2)n.

    ∴Sn=（n－1）(－2)n+1.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    （2013•金华模拟）己知等差数列{an}，公差d＞0，前n项和为Sn，且满足a2a3=45，a1+a4=14．
    （I）求数列{an}的通项公式及前，n项和Sn；
    （II）设bn=
    Sn
    n+c
    ，若数列{bn}也是等差数列，试确定非零常数c；并求数列{
    1
    bn•bn+1
    }    的前n项和Tn．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2013•烟台二模）己知等差数列{an}的首项为a1，公差为d，其前n项和为Sn，若直线y=a1x与圆（x-2）2+y2=1的两个交点关于直线x+y+d=0对称，则Sn=（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    己知等差数列{an}，公差d＞0，前n项和为Sn，且满足a2a3=45，a1+a4=14．
    （I）求数列{an}的通项公式及前，n项和Sn；
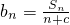    （II）设数学公式，若数列{bn}也是等差数列，试确定非零常数c；并求数列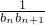数学公式的前n项和Tn．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    己知等差数列{an}的首项为a1，公差为d，其前n项和为Sn，若直线y=a1x与圆（x-2）2+y2=1的两个交点关于直线x+y+d=0对称，则Sn=（　　）
    A．n2B．-n2C．2n-n2D．n2-2n

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年浙江省金华市十校高三（下）4月联考数学试卷（文科）（解析版） 题型：解答题

    己知等差数列{an}，公差d＞0，前n项和为Sn，且满足a2a3=45，a1+a4=14．
    （I）求数列{an}的通项公式及前，n项和Sn；
    （II）设，若数列{bn}也是等差数列，试确定非零常数c；并求数列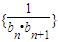的前n项和Tn．

    查看答案和解析>>

    同步练习册答案