Question

9．已知椭圆的左、右焦点为F₁、F₂，若椭圆上存在点P使∠F₁PF₂=60°，则椭圆的离心率的取值范围为（　　）

• A． [$\frac{\sqrt{3}}{2}$，1）
• B． （0，$\frac{\sqrt{3}}{2}$]
• C． [$\frac{1}{2}$，1）
• D． （0，$\frac{1}{2}$]

Answer 1

分析 当动点P在椭圆长轴端点处沿椭圆弧向短轴端点运动时，P对两个焦点的张角∠F₁PF₂渐渐增大，当且仅当P点位于短轴端点P₀处时，张角∠F₁PF₂达到最大值，由此可得结论．

解答 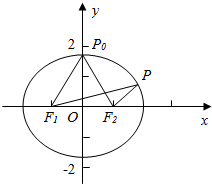解：如图，当动点P在椭圆长轴端点处沿椭圆弧向短轴端点运动时，
P对两个焦点的张角∠F₁PF₂渐渐增大，
当且仅当P点位于短轴端点P₀处时，张角∠F₁PF₂达到最大值．
∵存在点P为椭圆上一点，使得∠F₁PF₂=60°，
∴△P₀F₁F₂中，∠F₁P₀F₂≥60°，
∴Rt△P₀OF₂中，∠OP₀F₂≥30°，
所以P₀O≤$\sqrt{3}$OF₂，即b≤$\sqrt{3}$c，
∴a²-c²≤3c²，可得a²≤4c²，
∴$\frac{c}{a}$≥$\frac{1}{2}$，
∵0＜e＜1，
∴$\frac{1}{2}$≤e＜1．
故选C．

点评 本题考查了直角三角形的三角函数和椭圆的简单几何性质等知识点，考查数形结合的数学思想，属于中档题．