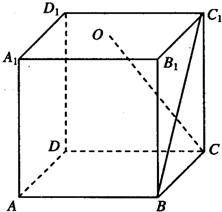
分析:建立如图的坐标系,以DA所在直线为横轴,DC所在直线为纵轴,DD1所在直线为竖轴,再给出各点的坐标,求出两个向量的坐标,利用公式求出夹角的余弦值即可.
解答:解:
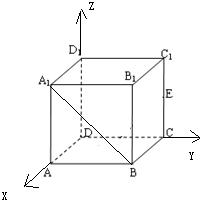
建立如图的坐标系,以DA所在直线为横轴,DC所在直线为纵轴,DD
1所在直线为竖轴.
设正方体棱长为a.
则A(a,0,0),D(0,0,0),C(0,a,0),B(a,a,0)C
1(0,a,a) A
1(a,0,a).
因为O为A
1,C
1的中点
∴O(
,
,a).
∴
=(-a,0,a),
=(-
,
,-a).
∴cos<
•>=
=
=-
.
∴异面直线OC与BC
1所成角的余弦值为
.
故答案为:
.
点评:本题考查用空间向量求直线间的夹角、距离,解答本题,关键是掌握住向量法求夹角的公式,向量在几何中的应用是高中数学引入向量的一大亮点,它大大降低了立体几何解题的思维难度,应好好总结此类题做题的规律.