Question

若实数x，y满足

2x-y≤0 x-3y+5≥0 x＞0，y＞0

，则（x+1）²+y²的最大值是（　　）

• A．2

  2

• B．8
• C．

  10

• D．

  34

  3

Answer 1

分析：先作出不等式组表示的平面区域，，令Z=（x+1）²+y²，则Z的几何意义是可行域内的任意一点与点（-1，0）的距离的平方，结合图形可求

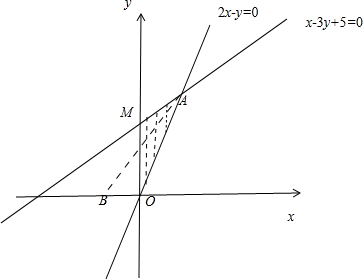
解答：解：作出不等式组表示的平面区域，如图所示
令Z=（x+1）²+y²，则Z的几何意义是可行域内的任意一点与点（-1，0）的距离的平方
由

2x-y=0 x-3y+5=0

可得A（1，2）
结合图形可知，所求的最大值为Z=|AB|²=（1+1）²+（2+0）²=8
故选B

点评：本题主要考查了线性规划知识的简单应用，解题的关键是明确目标函数的几何意义并准确判断出取得最值的位置．