
【题目】某班有学生50人,其中男同学30人,用分层抽样的方法从该班抽取5人去参加某社区服务活动.
(1)求从该班男女同学在各抽取的人数;
(2)从抽取的5名同学中任选2名谈此活动的感受,求选出的2名同学中恰有1名男同学的概率.
【答案】
(1)解:抽取的5人中男同学的人数为5× ![]() =3人,女同学的人数为5﹣3=2人.
=3人,女同学的人数为5﹣3=2人.
(2)解:记3名男同学为A1,A2,A3,2名女同学为B1,B2.
从5人中随机选出2名同学,所有可能的结果有A1A2,A1A3,A1B1,A1B2,A2A3,A2B1,A2B2,A3B1,A3B2,B1B2,共10个.
用C表示:“选出的两名同学中恰有一名男同学”这一事件,则C中的结果有6个,它们是A1B1,A1B2,A2B1,A2B2,A3B1,A3B2,
所以 选出的两名同学中恰有一名男同学的概率P(C)= ![]() =
= ![]()
【解析】(Ⅰ)按照分层抽样的方法:各层被抽到的比例相同解答;(Ⅱ)利用列举法分别明确从选出的5人中随机选出2名同学进行访谈和选出的两名同学中恰有一名男同学的所以可能,利用古典概率公式解答.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,正方体ABCD-A1B1C1D1 , O是底面ABCD对角线的交点.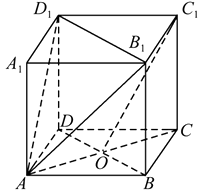
求证:(I) C1O∥面AB1D1;
(II)面A1C⊥面AB1D1 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)=x2﹣2x+3 (Ⅰ)若函数 ![]() 的最小值为3,求实数m的值;
的最小值为3,求实数m的值;
(Ⅱ)若对任意互不相同的x1 , x2∈(2,4),都有|f(x1)﹣f(x2)|<k|x1﹣x2|成立,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=sin(ωx+φ)(ω>0,|φ|< ![]() )的最小正周期为π,若其图象向左平移
)的最小正周期为π,若其图象向左平移 ![]() 个单位后得到的函数为奇函数,则函数f(x)的图象( )
个单位后得到的函数为奇函数,则函数f(x)的图象( )
A.关于点( ![]() ,0)对称
,0)对称
B.关于点(﹣ ![]() ,0)对称
,0)对称
C.关于直线x=﹣ ![]() 对称
对称
D.关于直线x= ![]() 对称
对称
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() 为偶函数.
为偶函数.
(1)求实数t值;
(2)记集合E={y|y=f(x),x∈{1,2,3}},λ=lg22+lg2lg5+lg5﹣1,判断λ与E的关系;
(3)当x∈[a,b](a>0,b>0)时,若函数f(x)的值域为[2﹣ ![]() ,2﹣
,2﹣ ![]() ],求实数a,b的值.
],求实数a,b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,内角A,B,C对边的边长分别是a,b,c,已知c=2, ![]() .
.
(1)若△ABC的面积等于 ![]() ,求a,b;
,求a,b;
(2)若sinB=2sinA,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】北京市为了缓解交通压力,计划在某路段实施“交通限行”,为调查公众对该路段“交通限行”的态度,某机构从经过该路段的人员中随机抽查了80人进行调查,将调查情况进行整理,制成表:
年龄(岁) | [15,30) | [30,45) | [45,60) | [60,75) |
人数 | 24 | 26 | 16 | 14 |
赞成人数 | 12 | 14 | x | 3 |
(1)若经过该路段的人员对“交通限行”的赞成率为0.40,求x的值;
(2)在(1)的条件下,若从年龄在[45,60),[60,75)内的两组赞成“交通限行”的人中在随机选取2人进行进一步的采访,求选中的2人中至少有1人来自[60,75)内的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com