
【题目】北京市为了缓解交通压力,计划在某路段实施“交通限行”,为调查公众对该路段“交通限行”的态度,某机构从经过该路段的人员中随机抽查了80人进行调查,将调查情况进行整理,制成表:
年龄(岁) | [15,30) | [30,45) | [45,60) | [60,75) |
人数 | 24 | 26 | 16 | 14 |
赞成人数 | 12 | 14 | x | 3 |
(1)若经过该路段的人员对“交通限行”的赞成率为0.40,求x的值;
(2)在(1)的条件下,若从年龄在[45,60),[60,75)内的两组赞成“交通限行”的人中在随机选取2人进行进一步的采访,求选中的2人中至少有1人来自[60,75)内的概率.
【答案】
(1)解:经过该路段的人员中对“交通限行”赞成的人数为12+14+x+3,
因为样本中的赞成率为0.40,所以 ![]() =0.40,解得x=3.
=0.40,解得x=3.
(2)解:记“选中的2人中至少有1人来自[60,75)内”为事件M.
设年龄在[45,60)内的3为调查者分别为A,B,C,年龄在[60,75)内的3为调查者分别为a,b,c,
则从这6位被调查者中抽出2人的情况有:
{a,b},{a,c},{a,A},{a,B},{a,C},{b,c},{b,A},{b,B},{b,C},{c,A},{c,B},{c,C},{A,B},{A,C},{B,C},
共15个基本事件,且每个基本事件等可能发生.
其中事件M包括{a,b},{a,c},{a,A},{a,B},{a,C},{b,c},{b,A},{b,B},{b,C},{c,A},{c,B},{c,C},共12个基本事件.
所以选中的2人中至少有1人来自[60,75)内的概率P(M)= ![]() .
.
【解析】(1)经过该路段的人员中对“交通限行”赞成的人数为12+14+x+3,由此利用样本中的赞成率为0.40,能求出x的值.(2)记“选中的2人中至少有1人来自[60,75)内”为事件M,设年龄在[45,60)内的3为调查者分别为A,B,C,年龄在[60,75)内的3为调查者分别为a,b,c,由此利用列举法能求出选中的2人中至少有1人来自[60,75)内的概率P(M).


 小学课时特训系列答案
小学课时特训系列答案科目:高中数学 来源: 题型:
【题目】某班有学生50人,其中男同学30人,用分层抽样的方法从该班抽取5人去参加某社区服务活动.
(1)求从该班男女同学在各抽取的人数;
(2)从抽取的5名同学中任选2名谈此活动的感受,求选出的2名同学中恰有1名男同学的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知偶函数f(x)和奇函数g(x)的定义域都是(﹣4,4),且在(﹣4,0]上的图象如图所示,则关于x的不等式f(x)g(x)<0的解集是 . 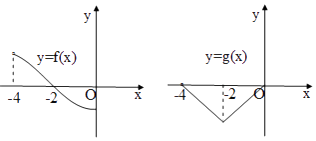
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,有一块半径为2的半圆形钢板,计划剪裁成等腰梯形ABCD的形状,它的下底AB是⊙O的直径,上底CD的端点在圆周上.设∠DAB=θ(0<θ< ![]() ),L为等腰梯形ABCD的周长.
),L为等腰梯形ABCD的周长. 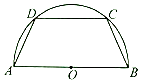
(1)求周长L与θ的函数解析式;
(2)试问周长L是否存在最大值?若存在,请求出最大值,并指出此时θ的大小;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地政府落实党中央“精准扶贫”政策,解决一贫困山村的人畜用水困难,拟修建一个底面为正方形(由地形限制边长不超过10m)的无盖长方体蓄水池,设计蓄水量为800m3 . 已知底面造价为160元/m2 , 侧面造价为100元/m2 . (I)将蓄水池总造价f(x)(单位:元)表示为底面边长x(单位:m)的函数;
(II)运用函数的单调性定义及相关知识,求蓄水池总造价f(x)的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在区间D上,如果函数f(x)为减函数,而xf(x)为增函数,则称f(x)为D上的弱减函数.若f(x)= ![]()
(1)判断f(x)在区间[0,+∞)上是否为弱减函数;
(2)当x∈[1,3]时,不等式 ![]() 恒成立,求实数a的取值范围;
恒成立,求实数a的取值范围;
(3)若函数g(x)=f(x)+k|x|﹣1在[0,3]上有两个不同的零点,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系内,已知A(3,3)是⊙C上一点,折叠该圆两次使点A分别与圆上不相同的两点(异于点A)重合,两次的折痕方程分别为x﹣y+1=0和x+y﹣7=0,若⊙C上存在点P,使∠MPN=90°,其中M、N的坐标分别为(﹣m,0)(m,0),则m的最大值为( )
A.4
B.5
C.6
D.7
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com