
【题目】某地政府落实党中央“精准扶贫”政策,解决一贫困山村的人畜用水困难,拟修建一个底面为正方形(由地形限制边长不超过10m)的无盖长方体蓄水池,设计蓄水量为800m3 . 已知底面造价为160元/m2 , 侧面造价为100元/m2 . (I)将蓄水池总造价f(x)(单位:元)表示为底面边长x(单位:m)的函数;
(II)运用函数的单调性定义及相关知识,求蓄水池总造价f(x)的最小值.
【答案】解:(Ⅰ)设蓄水池高为h,则 ![]() ,
,
∴ ![]()
= ![]()
(Ⅱ)任取x1,x2∈(0,10],且x1<x2,则 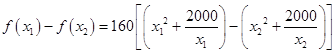
= 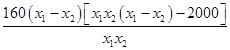
∵0<x1<x2≤10,∴x1x2>0,x1﹣x2<0,x1x2(x1+x2)<2000,
∴y=f(x1)﹣f(x2),即f(x1)>f(x2),∴y=f(x)在x∈(0,10]上单调递减
故x=10当时,fmin(x)=f(10)=48000
答:当底面边长为10m时,蓄水池最低造价为48000元
【解析】(I)设蓄水池高为h,则 ![]() ,利用底面造价为160元/m2,侧面造价为100元/m2,即可将蓄水池总造价f(x)(单位:元)表示为底面边长x(单位:m)的函数;(II)确定y=f(x)在x∈(0,10]上单调递减,即可求蓄水池总造价f(x)的最小值.
,利用底面造价为160元/m2,侧面造价为100元/m2,即可将蓄水池总造价f(x)(单位:元)表示为底面边长x(单位:m)的函数;(II)确定y=f(x)在x∈(0,10]上单调递减,即可求蓄水池总造价f(x)的最小值.
【考点精析】本题主要考查了基本不等式在最值问题中的应用的相关知识点,需要掌握用基本不等式求最值时(积定和最小,和定积最大),要注意满足三个条件“一正、二定、三相等”才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】函数f(x)=sin(ωx+φ)(ω>0,|φ|< ![]() )的最小正周期为π,若其图象向左平移
)的最小正周期为π,若其图象向左平移 ![]() 个单位后得到的函数为奇函数,则函数f(x)的图象( )
个单位后得到的函数为奇函数,则函数f(x)的图象( )
A.关于点( ![]() ,0)对称
,0)对称
B.关于点(﹣ ![]() ,0)对称
,0)对称
C.关于直线x=﹣ ![]() 对称
对称
D.关于直线x= ![]() 对称
对称
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知一组数据x1 , x2 , x3 , x4 , x5的平均数是2,方差是 ![]() ,那么另一组数据3x1﹣2,3x2﹣2,3x3﹣2, 3x4﹣2,3x5﹣2的平均数和方差分别是 .
,那么另一组数据3x1﹣2,3x2﹣2,3x3﹣2, 3x4﹣2,3x5﹣2的平均数和方差分别是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=loga ![]() ,g(x)=loga(x+2a)+loga(4a﹣x),其中a>0,且a≠1.
,g(x)=loga(x+2a)+loga(4a﹣x),其中a>0,且a≠1.
(1)求f(x)的定义域,并判断f(x)的奇偶性;
(2)已知区间D=[2a+1,2a+ ![]() ]满足3aD,设函数h(x)=f(x)+g(x),h(x)的定义域为D,若对任意x∈D,不等式|h(x)|≤2恒成立,求实数a的取值范围.
]满足3aD,设函数h(x)=f(x)+g(x),h(x)的定义域为D,若对任意x∈D,不等式|h(x)|≤2恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】北京市为了缓解交通压力,计划在某路段实施“交通限行”,为调查公众对该路段“交通限行”的态度,某机构从经过该路段的人员中随机抽查了80人进行调查,将调查情况进行整理,制成表:
年龄(岁) | [15,30) | [30,45) | [45,60) | [60,75) |
人数 | 24 | 26 | 16 | 14 |
赞成人数 | 12 | 14 | x | 3 |
(1)若经过该路段的人员对“交通限行”的赞成率为0.40,求x的值;
(2)在(1)的条件下,若从年龄在[45,60),[60,75)内的两组赞成“交通限行”的人中在随机选取2人进行进一步的采访,求选中的2人中至少有1人来自[60,75)内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=( ![]() )x的图象与函数y=g(x)的图象关于直线y=x对称,令h(x)=g(1﹣x2),则关于函数y=h(x)的下列4个结论: ①函数y=h(x)的图象关于原点对称;
)x的图象与函数y=g(x)的图象关于直线y=x对称,令h(x)=g(1﹣x2),则关于函数y=h(x)的下列4个结论: ①函数y=h(x)的图象关于原点对称;
②函数y=h(x)为偶函数;
③函数y=h(x)的最小值为0;
④函数y=h(x)在(0,1)上为增函数
其中,正确结论的序号为 . (将你认为正确结论的序号都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=b+logax(x>0且a≠1)的图象经过点(8,2)和(1,﹣1).
(1)求f(x)的解析式;
(2)[f(x)]2=3f(x),求实数x的值;
(3)令y=g(x)=2f(x+1)﹣f(x),求y=g(x)的最小值及其最小值时x的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的几何体中,四边形DCFE为正方形,四边形ABCD为等腰梯形,AB∥CD,AC= ![]() ,AB=2BC=2,且AC⊥FB.
,AB=2BC=2,且AC⊥FB. 
(1)求证:平面EAC⊥平面FCB;
(2)若线段AC上存在点M,使AE∥平面FDM,求 ![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com